Back to July Calendar	←Previous Entry	Next Entry→
September 03, 2005 What is a math parser?  It's an algorithm for taking a mathematical expression and assigning meaning to it.  The simplest place to start with with a 4 function calculator, which takes an expression involving operations on numbers and outputs a single number as the meaning, such as –4 + 2*(3 – 7)/8.  Let's introduce some key terms. Wow-somehow I've lost all my work of today after thinking I'd saved and rebooting.  Wow. Ok, so I'd gone Wikipedia and gotten the grasp of a dog biting a basketball on the massive complexity of parsing and lexical analysis.  For now, I'd just like to be able have code that takes an expression describing a function of a single variable, say, y = –1+ 2*(x - 3)^2/5, evaluates it over a sampling of x values and plots the (x,y) pairs.  That doesn't seem like too much to ask, does it? So the "push and operate" approach takes a mathematical expression represented as a string of symbols sorts them into to stacks: one for operands (numbers and variables) and the other for operations.  The operators can be classified by their position (before, after, between or surrounding the operands) and whether they take one (unary) or two (binary) operands. Type Arity Placement Examples prefix unary before the operand Unary minus postfix unary after the operand Factorial infix binary between operands Addition, multiplication, and division confix unary surrounding operand Parentheses, half-open ranges function application binary after first operand and surrounding second operand Mathematical functions, such as sin(x), and array indexed functions like a[5] Operands in the input stream are immediately put on the operand stack, while operators are put on the operator stack only if the operator stack is empty. If the operator stack is not empty, the following table determines the action of the parser depending on the type of the operator on top of the operator stack and on the type of the current operator token. "push" means to simply push the operator on the operator stack "operate" means to actually perform the operation, popping as many operands off the operand stack as needed, finally pushing the result of the operation back on the operand stack "ooops" (order of operations) means to compare the current operator with the operator on the top of the stack.  if the top of the operator stack has lower precedence than the current operator, push if the top of the operator stack has higher precedence than the current operator, operate if the ooops precedences are equal, then associativity is considered.  If the top of stack operator is left associative, then perform the operation--if it's right associative, push it on the operator stack. operator decision table   Current operator Prefix Postfix Infix Confix Open Confix/Function Close Function Open End of Input Top of Stack Prefix push ooops ooops push operate ooops operate Postfix - operate operate - operate operate operate Infix push ooops ooops/associativity push operate ooops operate Confix Open push push push push push push operate Confix/Function Close operate operate operate operate operate operate operate Function Open push push push push push push operate 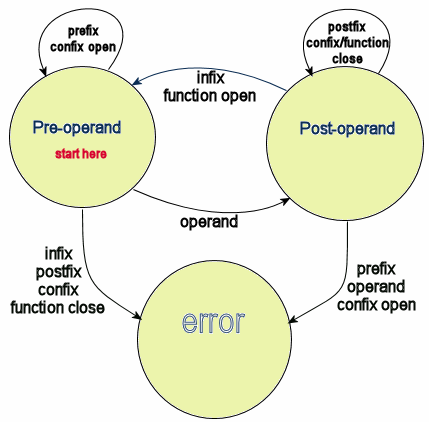It's important to know when an expression is invalid, such as +*5/0/x/0*1^8-*  and such.  Examine carefully the flow of symbols in a meaningful mathematical expression and patterns emerge as to what type of operator or operand can follow another.  The state diagram at right illustrates a good way of ensuring that the expression is valid.  There are three states: pre-operand, post-operand and error. Starting in pre-operand mode, there are three legal input possibilities: an operand, a prefix operator or a confix open operator.  If an operand is encountered, then the state goes to post operand mode; if a prefix is encountered, it's put on the operator stack and the state stays in per-operand mode--the same if a confix open symbol is encountered.  An expression cannot start with a binary operator, postfix operator or confix/function close symbol, so one of those will lead to the error state.  Suppose, for instance, we are processing the string –4+2*f(3–7)/8.  First the unary negation operator is put on the operator stack, then the operand 4 is put on the operand stack and the state is post-operand.  A binary infix sum operator is encountered.  Since the top of the operator stack contains a prefix operator, we use the order of operations as a guide.  Since unary negation takes precedence over binary sum, the negation operator is applied to 4 and so –4 is on the operand stack and + is pushed on the operator stack and the state is back to prefix mode.  Next, the operand 2 is put on the operand stack and the binary infix * operator is encountered, whose precedence is higher than the + currently on the operator stack, so push * on the operator stack.  We then have a function open and put 3 on the operand stack, flipping back and forth to post-operand mode again and then again to fetch the minus seven, causing the operation and then leaving another –4 on the operand stack.  So far the stacks are operands: –4,2,–4 operators: +*f Now the / operator is encountered, and thus f(–4) must be evaluated and put on the operand stack: operands: –4,2,f(–4) operators: +* and since * and / have equal precedence, the multiplication is done before the division and we have operands: –4,2*f(–4)/8 operators: + Finally the addition operator acts on the two remaining operands. As excruciating simple as this seems, there are problems that come up, not least of which are ambiguous cases where an operator can have different meaning in different cases: the unary negation and binary minus both use the same symbol, for instance.  And the absolute value uses the same symbol to open and close.  Given an operator name, we can determine the set of operator types to which it may belong and then compare these with the operator types that are valid in the current mode of the state machine.  This process is referred to by the ungainly polysyllabic, "disambiguation." Sometimes a disambiguation requires looking ahead through the string. Here's an interesting illustration of this process, which I found here. Parse the expression x * |y+z| + -3^x^y using the standard mathematical rules for precedence and associativity. State Operand Stack Operator Stack Token Token type Action Pre     x operand shift Post x   * infix operator shift Pre x * | confix open or confix close disambiguate as confix open, shift Pre x * (confix open |) y operand shift Post x y * (confix open |) + infix or prefix operator disambiguate as infix, shift Pre x y * (confix open |) + z operand shift Post x y z * (confix open |) (infix +) | confix open or confix close disambiguate as close, reduce Post x (y+z) * (confix open |) | confix open or confix close disambiguate as close, reduce Post x (|y+z|) * + infix or prefix disambiguate as infix, compare precedence, reduce Post (x * (|y+z|))   + infix or prefix disambiguate as infix, shift Pre (x * (|y+z|)) (infix +) - infix or prefix disambiguate as prefix, shift Pre (x * (|y+z|)) (infix +) (prefix -) 3 operand shift Post (x * (|y+z|)) 3 (infix +) (prefix -) ^ infix compare precedence, shift Pre (x * (|y+z|)) 3 (infix +) (prefix -) ^ x operand shift Post (x * (|y+z|)) 3 x (infix +) (prefix -) ^ ^ infix compare precedence, compare associativity, shift Pre (x * (|y+z|)) 3 x (infix +) (prefix -) ^ ^ y operand shift Post (x * (|y+z|)) 3 x y (infix +) (prefix -) ^ ^ end end reduce Post (x * (|y+z|)) 3 (x^y) (infix +) (prefix -) ^ end end reduce Post (x * (|y+z|)) (3^(x^y)) (infix +) (prefix -) end end reduce Post (x * (|y+z|)) (-(3^(x^y))) (infix +) end end reduce Post ((x * (|y+z|)) + (-(3^(x^y)))) empty end end accept   http://www.cs.rpi.edu/~gregod/Sugar/doc/design.html update20140925: https://github.com/alex/django-templatetag-sugar/blob/master/templatetag_sugar/parser.py ? http://amath.colorado.edu/faculty/sherod/classes/Plotter/graph.html http://www.singularsys.com/jep/exampleapplets.html http://www.crbond.com/parsers.htm