August 24, 2005
The next part of solving the probability problem I set out a week or so ago is proving to be cantankerously obstreperous. The problem, to be sure, is, given a random set of 3 vertices in a unit square, what are the areas of shadow polygons, by which I mean the polygonal regions outside the triangle where a fourth vertex would not complete a convex quadrilateral.
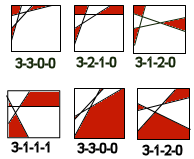
I thought mebbe one could use information about how the edge points are distributed around the perimeter of the unit square to determine what sort of polygonal shadows occur, but, as the diagram here show, that doesn't seem likely.
| The numbers below each square indicate the distribution
of edge vertices, starting with the left side and going
around clockwise. This is only a small sampling of the
possibilities, of course, but it shows some of the potential
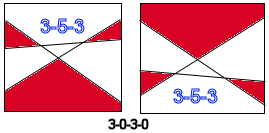
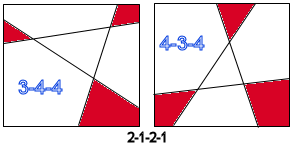
complexity. Notice that the two 3-3-0-0 entries have quite
different shadow polygons: the first has two triangles and a
quadrilateral and the other, two triangles and a hexagon. How about a simpler sub-problem? How many ways are there to draw two line segments intersecting on the interior of a square? Two configurations will only be considered different if one cannot be obtained from the other by |
 |
-
Sliding vertices along an edge (but not to a new edge.)
-
Rotating and/or flipping the square.
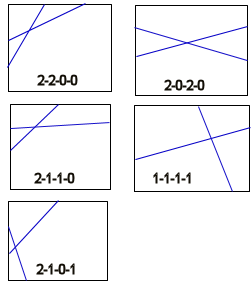
| There are 5 different ways that I can find
(shown at right.) This is equivalent to saying how
many ways are there to write 4 numbers, each 0, 1 or 2,
whose sum is 4. Two such sequences are different only
if one can't be obtained from the other by "rotating" or
reversing the sequence.
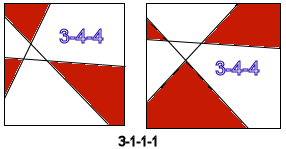
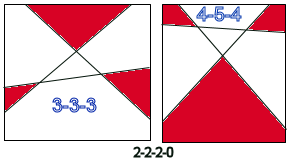
We can list all 9 possible arrangements of edge points
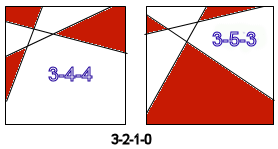
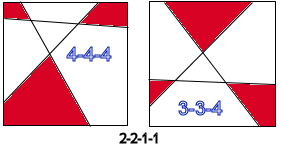
around the perimeter like so: For each we'd like to know how many different shadow polygon outcomes are possible. For instance, for the first (3-3-0-0) we have two, as described above. For 3-2-1-0, as shown below, there are either 3-gon, 4-gon, 4-gon (red) shadowgons, or 3-gon, 3-gon and 5-gon shadowgons. When compared with 3-3-0-0 pair, I have a way of saying which is which: is the intersection of 1st and 3rd edges(counting x1, x2, x3 from left to right) above or below the line emanating from the 2nd left edgepoint? |
 |
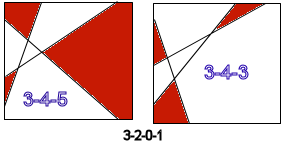
3-1-2-0 is obtained from 3-2-1-0 by moving the right-most vertex on the top edge further right and down around the upper right corner, so it's situation is pretty much the same as 3-2-1-0.
Truth be told, after making all
these diagrams, I'm pretty tired of the nitty gritty. Maybe
I'll come back to this with a fresh mind later on. For now,
the tedium of this makes me think moving on to parsing would be a
good thing.
 |
 |
 |
 |
 |
 |
 |
|