The 1969 Encyclopedia Britannica entry under "tide:"
[Page1] [Page2]
[Page3] [Page4]
[Page5] [Page6]
[Page7] [Page8]
DYNAMICS OF OCEAN TIDES
Equations of Motion.--The dynamical theory of tides introduced
by Laplace in the 18th century has given much insight into the problem
of tides in the ocean. The following assumptions and approximations are
commonly introduced:
(1) The water is assumed to be homogeneous; (2) vertical displacements
and velocities of the water particles are assumed small in comparison to
the horizontal displacements and velocities; (3) the water pressure at
any point in the water is given adequately by the hydrostatic law; i.e.,
it is equal to the head of water above the given point; (4) all dissipative
forces are neglected; and (5) the ocean basins are assumed rigid (as if
there were no bodily tide), and the gravitational potential of the tidally
displaced masses is neglected.
If assumptions (1) and (3) are valid it can readily be shown that the
tidal currents at any locality are uniform with depth.
Take a to denote the radius of the earth and g the acceleration
of gravity at its surface. Position on the earth's surface will be
designated by the longitude 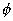 and the co-latitude (angular distance from the north pole to the point
under consideration)
and the co-latitude (angular distance from the north pole to the point
under consideration) 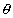 . Let h denote the depth of the ocean at any point, so that h is
a function of
. Let h denote the depth of the ocean at any point, so that h is
a function of 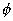 and
and 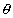 . Also,
let
. Also,
let 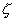 denote
the elevation of the free surface at any point of the ocean above its mean
level, and u and v the southward and eastward components
of the tidal current, so that these three quantities are functions of
denote
the elevation of the free surface at any point of the ocean above its mean
level, and u and v the southward and eastward components
of the tidal current, so that these three quantities are functions of 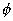 ,
,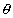 as well as of the time t. Then the equation of continuity, which
expresses the condition that the volume of any mass of water must remain
constant, may be written in the form (1)
as well as of the time t. Then the equation of continuity, which
expresses the condition that the volume of any mass of water must remain
constant, may be written in the form (1)
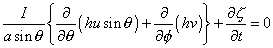 provided that the elevation of the sea surface is everywhere small compared
to the depth of water. If this is not the case then h must be replaced
by h +
provided that the elevation of the sea surface is everywhere small compared
to the depth of water. If this is not the case then h must be replaced
by h + 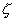 in equation (I). This equation may be derived by expressing the condition
that the net rate at which volume of water enters the sides of a vertical
column is equal to the rate of increase of the volume at the top of this
column by virtue of the time rate of increase of the elevation of the sea
surface
in equation (I). This equation may be derived by expressing the condition
that the net rate at which volume of water enters the sides of a vertical
column is equal to the rate of increase of the volume at the top of this
column by virtue of the time rate of increase of the elevation of the sea
surface 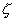 . Along
a coast line the condition that the tidal current have no comporient perpendicular
to the coast must be satisfied.
. Along
a coast line the condition that the tidal current have no comporient perpendicular
to the coast must be satisfied.
The equations of motion are formed by equating the southward and eastward
components of acceleration of the water particles to the sum of all the
forces per unit mass acting on the water in the southward and eastward
directions, respectively. The acceleration consists of three parts: the
local acceleration; the field acceleration; and the Coriolis acceleration
resulting from the earth's rotation. As an example, the southward component
of acceleration is equal to
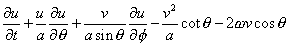 where, the first term represents the local, the second, third and fourth
terms combined represent the field, and the last term the Coriolis accelerations,
respectively. Here
where, the first term represents the local, the second, third and fourth
terms combined represent the field, and the last term the Coriolis accelerations,
respectively. Here 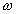 represents the angular speed of the earth's rotation. At this point an
additional assumption shown to be valid for tidal motion in true oceanic
regions is introduced: that the field acceleration is negligible as compared
to the local acceleration. In accordance with the foregoing approximations,
the only forces acting on the water are the tide-generating forces and
those attributable to the pressure gradient resulting from the slope of
the sea surface. The southward and eastward components of the pressure
gradient are given by
represents the angular speed of the earth's rotation. At this point an
additional assumption shown to be valid for tidal motion in true oceanic
regions is introduced: that the field acceleration is negligible as compared
to the local acceleration. In accordance with the foregoing approximations,
the only forces acting on the water are the tide-generating forces and
those attributable to the pressure gradient resulting from the slope of
the sea surface. The southward and eastward components of the pressure
gradient are given by
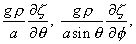
 being the water
density, and the southward and eastward components of the tide-generating
force are given by
being the water
density, and the southward and eastward components of the tide-generating
force are given by
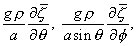 where
where  represents
the elevation of the equilibrium tide. This quantity is a function of
represents
the elevation of the equilibrium tide. This quantity is a function of 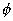 ,
,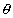 and t and is assumed known as it can be deduced from knowledge of
the relative movements of the earth, moon and sun. The equations of motion
can then be written in the form (2)
and t and is assumed known as it can be deduced from knowledge of
the relative movements of the earth, moon and sun. The equations of motion
can then be written in the form (2)
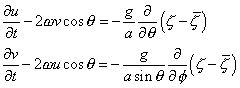 The equations (1) and (2) serve to determine completely, at least in theory,
the tidal currents and elevation over the entire oceans and for all times,
given a complete description of the tide-generating forces and the boundaries
of the ocean basins. In practice, however, such a general solution has
never been obtained owing to the complicated nature of the distribution
of sea and land masses and the varying depth of water. For this reason
tidal research has been based primarily on observations and general principles
(such as linearity, etc.) derived from theory.
The equations (1) and (2) serve to determine completely, at least in theory,
the tidal currents and elevation over the entire oceans and for all times,
given a complete description of the tide-generating forces and the boundaries
of the ocean basins. In practice, however, such a general solution has
never been obtained owing to the complicated nature of the distribution
of sea and land masses and the varying depth of water. For this reason
tidal research has been based primarily on observations and general principles
(such as linearity, etc.) derived from theory.
It may be noted that these equations are linear in u, v, 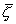 and with the result that the tide-generating forces may be separated into
several constituents, the sum of whose effects is exactly equivalent to
the effect produced by the sum total of all the tide-generating constituents.
Indeed, as has already been pointed out, this is the basis of the harmonic
development of the tide. Let us review under what conditions the ocean
tide is truly linear and under what conditions this linearity breaks down.
Unless the elevation of the sea surface above its mean position is always
small as compared to the mean depth h, equation (1) becomes nonlinear.
Similarly, if the field acceleration becomes so large it is no longer negligible
as compared to the local acceleration equations (2) become nonlinear. This
is most likely to occur in regions of large tidal currents with a large
spatial rate of change (current
shear). Nonlinear dissipative forces may be another source of nonlinearity.
All these effects are quite small in the vast oceanic regions but tend
to become larger in regions of shallow water and in the vicinity of the
coast line, and consequently are referred to as shallow-water tides.
and with the result that the tide-generating forces may be separated into
several constituents, the sum of whose effects is exactly equivalent to
the effect produced by the sum total of all the tide-generating constituents.
Indeed, as has already been pointed out, this is the basis of the harmonic
development of the tide. Let us review under what conditions the ocean
tide is truly linear and under what conditions this linearity breaks down.
Unless the elevation of the sea surface above its mean position is always
small as compared to the mean depth h, equation (1) becomes nonlinear.
Similarly, if the field acceleration becomes so large it is no longer negligible
as compared to the local acceleration equations (2) become nonlinear. This
is most likely to occur in regions of large tidal currents with a large
spatial rate of change (current
shear). Nonlinear dissipative forces may be another source of nonlinearity.
All these effects are quite small in the vast oceanic regions but tend
to become larger in regions of shallow water and in the vicinity of the
coast line, and consequently are referred to as shallow-water tides.
As to the other approximations, that of neglecting all dissipative mechanisms
(4) is not a very good one, but more will be said about this point in the
section on Tidal Friction. The bodily tides of the earth invalidate to
a certain extent assumption (5) by virtue of a small variable movement
of the sea floor and of the earth's own gravitational field. If 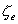 ,
designates the variable elevation of the sea floor above its mean position,
equation (1) will stand unaltered if we take
,
designates the variable elevation of the sea floor above its mean position,
equation (1) will stand unaltered if we take 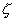 to denote the elevation of the sea surface relative to the sea floor, but
in the formulas for pressure gradients
to denote the elevation of the sea surface relative to the sea floor, but
in the formulas for pressure gradients 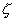 must be replaced by
must be replaced by 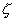 +
+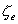 .
The disturbance n the gravitational forces brought about by the displacements
of water and solid earth must be accounted for by adding a term
.
The disturbance n the gravitational forces brought about by the displacements
of water and solid earth must be accounted for by adding a term 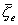 ,
to
,
to 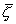 . Inhomogeneities
in the sea water have been neglected according to assumption (1), but may
have a more important effect in tidal motions than has been anticipated.
At any given time of the year a large part of the ocean is covered by a
nearly homogeneous layer of light, warm water 50 to 200 meters thick. Such
stratification of the sea water may influence the vertical structure of
the tidal current with resulting deviations from their generally assumed
uniformity with depth. Bottom friction will also introduce vertical shear
in the tidal current.
. Inhomogeneities
in the sea water have been neglected according to assumption (1), but may
have a more important effect in tidal motions than has been anticipated.
At any given time of the year a large part of the ocean is covered by a
nearly homogeneous layer of light, warm water 50 to 200 meters thick. Such
stratification of the sea water may influence the vertical structure of
the tidal current with resulting deviations from their generally assumed
uniformity with depth. Bottom friction will also introduce vertical shear
in the tidal current.
Suppose now that we consider the ocean's response to one harmonic constituent
of the equilibrium tide. If we take a long-period constituent, 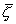 will have the form of a standing wave over the entire earth. A constituent
of any other species will have the form of a progressive wave rotating
relative to the earth about its axis in the westward direction. Such progressive
waves can, however, be expressed as the sum of two standing waves separated
in longitude by 90°, and separated in time also by 90°. In any
case, therefore. it will suffice to express
will have the form of a standing wave over the entire earth. A constituent
of any other species will have the form of a progressive wave rotating
relative to the earth about its axis in the westward direction. Such progressive
waves can, however, be expressed as the sum of two standing waves separated
in longitude by 90°, and separated in time also by 90°. In any
case, therefore. it will suffice to express 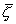 in the form
in the form
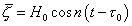 where n and
where n and 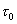 ,
are absolute constants and H is a function of geographic position but independent
of time. The actual response of the ocean will then be the sum of a number
of solutions to such inputs. The solutions for the tidal elevation
,
are absolute constants and H is a function of geographic position but independent
of time. The actual response of the ocean will then be the sum of a number
of solutions to such inputs. The solutions for the tidal elevation 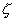 and current u, V from equations (1) and (2) will have the
form
and current u, V from equations (1) and (2) will have the
form


(2) where H, U, V, 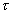 ,
, 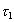 , and
, and 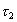 are all functions of geographical position only. While it is not feasible
to actually determine these functions analytically, if their values are
determined for a certain location on the earth by appropriate analysis
of tidal observation the response to the constituent under consideration
could be predicted for all time. In the case of the tidal elevation, wherever
H
and T have been determined for all important constituents, tht tidal
elevations there can be predicted for any time. It rqay bt remarked that
at a given place H0, and H are generally quite
different; i.e., the true tide bears little resemblance to the equilibrium
tide.
are all functions of geographical position only. While it is not feasible
to actually determine these functions analytically, if their values are
determined for a certain location on the earth by appropriate analysis
of tidal observation the response to the constituent under consideration
could be predicted for all time. In the case of the tidal elevation, wherever
H
and T have been determined for all important constituents, tht tidal
elevations there can be predicted for any time. It rqay bt remarked that
at a given place H0, and H are generally quite
different; i.e., the true tide bears little resemblance to the equilibrium
tide.
Nonlinear Distortion (Shallow-Water Tides)-At places where the
tidal elevation becomes appreciable as compared to the water depth,
or other nonlinear effects occur, the principle of superposition breaks
down. One might think that under these circumstances the concept of harmonic
constituents would be completely useless, but it has been found possible
to retain this concept provided that additional constituents, the so-called
shallow-water tides, be included. The regions where this phenomenon occurs
are generally confined to rivers, estuaries and shallow gulfs. The shallow-water
constituents are not produced by the direct action of the tide-generating
forces, but by the distortion, attributable to shoal water, of already
existing tidal constituents which have been formed in the ocean. In fact,
if the region of distortion is small enough (as it usually is), the tide-generating
forces have little or no direct effect on the shallow-water tide.
It is no longer correct
to consider separately the reactions to individual equilibrium constituents,
but let us take the simple example of only one equilibrium constituent
in order to gain insight into the problem. The response of a nonlinear
system to the harmonic forcing constituent will not be harmonic, but at
least it will be periodic, having the same period as the forcing or primary
constituent. If

is the period of the primary constituent, it is well known from the theory
of Fourier series that a periodic function of this period can be expressed
as the sum of purely harmonic terms having speeds a
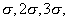
etc. Extending this idea to the actual situation one should expect to find shallow-water constituents having periods
of one-half, one-third, etc., of those of the major tidal constituents.
The shallow-water constituents obtained in this way are called
overtides
because of their analogy to overtones in acoustics. The same symbol is
used to designate these overtides as is used to designate the equilibrium
constituent which gives rise to them, and again the subscript designates
the species (approximate number of periods in a day) to which the overtide
belongs. For example the constituent
M2 gives
rise to the series of overtides
M4, M6,
etc.,
and
K1 gives rise to the overtides
K2,
K8, etc. In some cases an overtide will have exactly
the same period as another equilibrium constituent and it will be impossible
to separate the two by harmonic analysis. For example,
K2represents
the lunisolar semidiurnal constituent, but an overtide of exactly the same
period as
K2 is produced by nonlinear distortion
of the lunisolar diurnal constituent
K1. In this and
in similar cases the symbol
K2 (referring to the
actual tide) represents the combined effect of both the linear reaction
to the equilibrium constituent
K2and the overtide.
The theory of progressive
shallow-water waves of finite height has been used to estimate the relationship
between the amplitudes of the overtides and primary tide. The amplitude
of the nth overtide is found to be proportional to the nth
power of the amplitude of its primary at any given place, as the amplitude
of the primary varies in time. For example, if the range of the semidiurnal
tide is twice as great during the spring tides as during the neap tides,
the range of the quarter-diurnal overtide resulting from distortion of
the semidiurnal tide will be approximately four times as great during the
spring tides as during the neaps. The range of the 6-diurnal overtides
will be eight times as great during the spring tides, etc. As to the 19-year
nodal variation in amplitude, the node factors f of the overtides
bear a relation to those of the primary as illustrated in the following
example in the case of the overtides of the constituent M2:
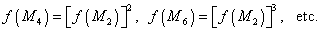
The above relations seem
to be confirmed fairly well in most cases by tidal observations in spite
of the fact that assumptions in the theory from which they have been derived
are far from fulfilled. For example, in many regions where overtides are
important, such as some rivers and estuaries, the tidal wave has more nearly
the form of a standing wave than that of a progressive wave, but the theory
for standing shallow-water waves of finite height has not been adequately
developed. Also, the nonlinear effects caused by one constituent cannot,
strictly speaking, be superimposed on those caused by another.
The nonlinear interaction
between two or more primary constituents can be accounted for by the inclusion
of compound constituents. In the case of two interacting primary constituents
having speeds al and
0?2, a series of compound constituents will
result, having speeds
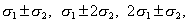
etc.,
including all possible combinations of the form
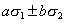
,
where
a and
b are integers. The relationship of the amplitudes
of the compound constituents to those of their primaries has been approximated
by assuming that the system responds like a power-law filter; i.e., like
a system whose output is equal to a polynomial function of the input. In
this way the relative importance of the compound constituents of any given
species as well as the dependence of their node factors on those of the
primary constituents can be evaluated. No general conclusions can be drawn
concerning the relative importance of two compound constituents belonging
to different species.
|
Symbol
|
Speed
|
Speed in °/hr.
|
Node factor
|
|
2SM2
|
|
31.016
|
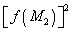
|
|
MNS2
|
|
27.424
|

|
|
MK3
|
|
44.025
|
|
|
MK3
|
|
42.927
|
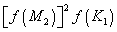
|
|
M4
|
|
57.968
|
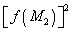
|
|
MS4
|
|
58.984
|

|
Table II includes the more important shallow-water constituents, both
overtides and compound constituents. In the table, only two of each of
the semidiurnal, terdiurnal and 4-diurnal shallow-water constituents are
given for illustration, but there are ports for which many others would
be needed to give an accurate representation of the tide. In fact for some
ports the number of these constituents that would be needed is so high
that the harmonic method becomes impractical. It may be noted that the
two terdiurnal constituents listed in Table II are given the same symbol.
Actually there is some confusion as to the designation of the compound
constituents. The designations given in Table II are based on the nomenclature
used by the United States coast and geodetic survey.
![]() and the co-latitude (angular distance from the north pole to the point
under consideration)
and the co-latitude (angular distance from the north pole to the point
under consideration) ![]() . Let h denote the depth of the ocean at any point, so that h is
a function of
. Let h denote the depth of the ocean at any point, so that h is
a function of ![]() and
and ![]() . Also,
let
. Also,
let ![]() denote
the elevation of the free surface at any point of the ocean above its mean
level, and u and v the southward and eastward components
of the tidal current, so that these three quantities are functions of
denote
the elevation of the free surface at any point of the ocean above its mean
level, and u and v the southward and eastward components
of the tidal current, so that these three quantities are functions of ![]() ,
,![]() as well as of the time t. Then the equation of continuity, which
expresses the condition that the volume of any mass of water must remain
constant, may be written in the form (1)
as well as of the time t. Then the equation of continuity, which
expresses the condition that the volume of any mass of water must remain
constant, may be written in the form (1)
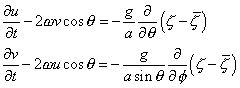
![]() and with the result that the tide-generating forces may be separated into
several constituents, the sum of whose effects is exactly equivalent to
the effect produced by the sum total of all the tide-generating constituents.
Indeed, as has already been pointed out, this is the basis of the harmonic
development of the tide. Let us review under what conditions the ocean
tide is truly linear and under what conditions this linearity breaks down.
Unless the elevation of the sea surface above its mean position is always
small as compared to the mean depth h, equation (1) becomes nonlinear.
Similarly, if the field acceleration becomes so large it is no longer negligible
as compared to the local acceleration equations (2) become nonlinear. This
is most likely to occur in regions of large tidal currents with a large
spatial rate of change (current
shear). Nonlinear dissipative forces may be another source of nonlinearity.
All these effects are quite small in the vast oceanic regions but tend
to become larger in regions of shallow water and in the vicinity of the
coast line, and consequently are referred to as shallow-water tides.
and with the result that the tide-generating forces may be separated into
several constituents, the sum of whose effects is exactly equivalent to
the effect produced by the sum total of all the tide-generating constituents.
Indeed, as has already been pointed out, this is the basis of the harmonic
development of the tide. Let us review under what conditions the ocean
tide is truly linear and under what conditions this linearity breaks down.
Unless the elevation of the sea surface above its mean position is always
small as compared to the mean depth h, equation (1) becomes nonlinear.
Similarly, if the field acceleration becomes so large it is no longer negligible
as compared to the local acceleration equations (2) become nonlinear. This
is most likely to occur in regions of large tidal currents with a large
spatial rate of change (current
shear). Nonlinear dissipative forces may be another source of nonlinearity.
All these effects are quite small in the vast oceanic regions but tend
to become larger in regions of shallow water and in the vicinity of the
coast line, and consequently are referred to as shallow-water tides.
![]() ,
designates the variable elevation of the sea floor above its mean position,
equation (1) will stand unaltered if we take
,
designates the variable elevation of the sea floor above its mean position,
equation (1) will stand unaltered if we take ![]() to denote the elevation of the sea surface relative to the sea floor, but
in the formulas for pressure gradients
to denote the elevation of the sea surface relative to the sea floor, but
in the formulas for pressure gradients ![]() must be replaced by
must be replaced by ![]() +
+![]() .
The disturbance n the gravitational forces brought about by the displacements
of water and solid earth must be accounted for by adding a term
.
The disturbance n the gravitational forces brought about by the displacements
of water and solid earth must be accounted for by adding a term ![]() ,
to
,
to ![]() . Inhomogeneities
in the sea water have been neglected according to assumption (1), but may
have a more important effect in tidal motions than has been anticipated.
At any given time of the year a large part of the ocean is covered by a
nearly homogeneous layer of light, warm water 50 to 200 meters thick. Such
stratification of the sea water may influence the vertical structure of
the tidal current with resulting deviations from their generally assumed
uniformity with depth. Bottom friction will also introduce vertical shear
in the tidal current.
. Inhomogeneities
in the sea water have been neglected according to assumption (1), but may
have a more important effect in tidal motions than has been anticipated.
At any given time of the year a large part of the ocean is covered by a
nearly homogeneous layer of light, warm water 50 to 200 meters thick. Such
stratification of the sea water may influence the vertical structure of
the tidal current with resulting deviations from their generally assumed
uniformity with depth. Bottom friction will also introduce vertical shear
in the tidal current.
![]() will have the form of a standing wave over the entire earth. A constituent
of any other species will have the form of a progressive wave rotating
relative to the earth about its axis in the westward direction. Such progressive
waves can, however, be expressed as the sum of two standing waves separated
in longitude by 90°, and separated in time also by 90°. In any
case, therefore. it will suffice to express
will have the form of a standing wave over the entire earth. A constituent
of any other species will have the form of a progressive wave rotating
relative to the earth about its axis in the westward direction. Such progressive
waves can, however, be expressed as the sum of two standing waves separated
in longitude by 90°, and separated in time also by 90°. In any
case, therefore. it will suffice to express ![]() in the form
in the form
![]()
![]()