Back to November Calendar            ←Previous Entry                             Next Entry→

November 9, 2005

Spline Representations I

 

I google “spline” and I get http://www.mathworks.com/products/splines/ as the second hit (the first hit brings up a university site that informs me how I don’t have access to itI ain’t no priviledged son, no, no.)  But I want to invent my own wheel using freeware OpenGL code, so there.

 

 A better link is http://www.saltire.com/applets/advanced_geometry/spline/spline.htm which is a very nice interactive applet with a succinct explanation of spline it illustrates.

 

Here’s another good one: http://www.math.ucla.edu/~baker/java/hoefer/Spline.htm .

 

Splines were invented out of a need to draw approximating curves with a minimum of computation.  Most students first get a hint of this when they study Simpson’s method in calculus.  With Simpson’s method a function is sampled and the samples are grouped to fit parabolas to adjacent sets of three and the area under the curve can be approximated as the sum of areas under the adjacent parabolas, which, after considerable simplification, comes to the simple formula

                          

The simplest sort of splines typically takes up where this leaves off: by fitting a cubic to adjacent sets of three, with the added condition that the slopes of the tangent lines to the curve and the approximating cubic agree at the splice, so the curve is smooth throughout.

 

OpenGL’s POLY_LINE is the sequence of connected line segments connecting a given set of points.  From the perspective of splines, this called the control polygon or control graph (since it’s not actually a polygon, is it?)

 

If we parameterize a space curve

                                             

we can impose parametric continuity conditions by equating parametric derivatives of adjacent curve sections at their common boundary.

 

The zero-order continuity condition, C0, is simply that the curves connect; that the right endpoint of one section meets the left endpoint of the next section: v(t2) = v(t1).  The first-order continuity condition requires that the tangent line (directional derivatives) agree.  The second-order continuity condition requires that the curves meet and the 1st and 2nd order parametric derivatives agree. 

 

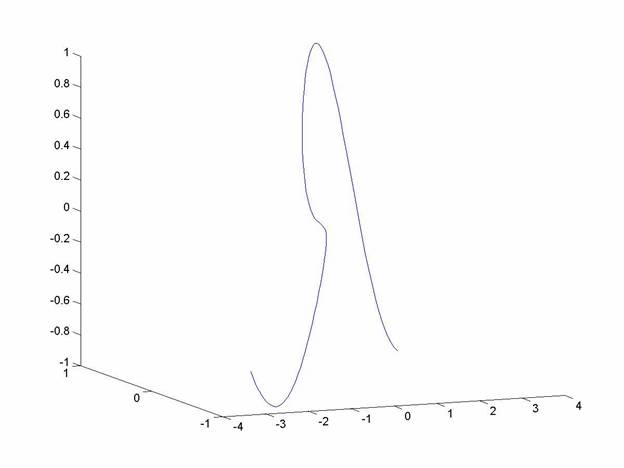
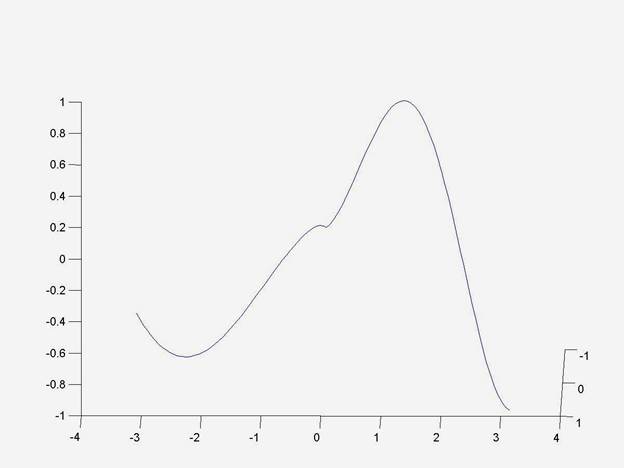
Example   The vector valued space curve  is certainly continuous at the origin since , however, dy/dt is not defined at the origin, so the curve does not meet the first order continuity condition at the origin.  To get a handle on what this curve looks like, we could use MatLab to first define a partition of the interval from −π to π through steps of π /50 like so:

 

     t = -pi:pi/50:pi;

 

and then plot the space curve using these commands (“real” is needed to force the real root):

 

     plot3(t,sin(real(t^(2/3))),sin(real(t^(4/3))))

     axis square

     grid on

 

the plot can then be rotated by clicking and dragging on it.  From this perspective, it looks pretty smooth, though there is evidence of a kink at the origin. 

Rotate the camera a bit and you see the kink more clearly:

A second-order discontinuity is very hard to see this way, so first-order continuity is usually sufficient for rendering smooth curves and surfaces.

 

Further, we can relax the condition a bit by require only that the derivatives have the same direction, but not necessarily the same magnitude.  This is called the geometric continuity condition.   The condition for zero-order geometric continuity, G0,  is the same as that for zero-order parametric continuity: that the curves at the boundary.  The G1 condition is that the tangent lines of two successive parametric pieces are parallel.  The G2 condition is that the two curves have the same curvature: again, this requirement is usually unnecessary for the purpose of a visually smooth curve or surface.  Generally, the a curve meeting the geometric continuity condition, but not the parametric continuity condition will pass through the same control points, but have a somewhat different shape.

 

 

For example, if we want to construct a quadratic spline for a curve y = f(x), we can compute coordinates of three points on the curve, say,

                                               

and then define

                                                               

so that

 

is a system of equations we can solve for the vector coefficients a0, a1 and a2: 

 

                                                           

========================================================

For a given set of control points (boundary points) and a degree for the polynomials we want to patch together, there are three main ways to specify a spline:

  1. Specify the boundary conditions (G1, say.)
  2. Write the matrix used to do the spline computations.
  3. State the blending functions (aka basis functions) that are used to meet constraints.

 

As an example, a section of cubic spline can be represented as

                              

where B is a column vector representing the boundary points and A is the 4x4 transformation to spline form matrix.  This is actually what’s termed a change of basis matrix in linear algebra? 

 

We can also think of this as getting a polynomial representation of a particular coordinate (say, y, of (x,y,z)) in terms of the boundary parameters bk by choosing the right blend of polynomials like so:

                                                                 

Where Pk(t) are the blending (basis) polynomials.

 

I’ll admit that last bit was too slick and quickfor me, at least.  Let’s try again, from the beginning.  Let’s say we have a set of control points along a vector valued function  

                                                  

that correspond to the partition

                                                                 

We can reduce the problem to interpolating x(t) using cubic splines with, say,

                                  

which, conveniently, meets the boundary condition

                                                                       

There will be n−1 splices with 3 unknown coefficients per splice, making 2n−1 coefficients to be determined, meeting the other boundary constraints:

                                                           

and, to meet the n−2 first-order continuity constraints,

                                                      

or, in dot-hat notation,

                                                                  

For second-order continuity, require that

                                                                  

To simplify notation, let .  Then the zero-order conditions are

,

and first-order conditions are

 

while the second-order conditions are

 

Further, the conditions for a “natural spline” require that the curve begins and ends with curvature zero means

                                                        

 

Summing up, we have the following system:

                                                

 

For simplicity, here’s the matrix version of this system when n = 3:

                                          

It turns out the computation can be made more efficient by considering both endpoint of a sub-interval.  Consider this form of the cubic spline (note this s is not the s above):

EQ1                          

The first and second derivatives for k = 1, 2, …, n-1 are

                                                

Thus , and since this agrees with , the second derivatives agree at the interior control points by construction. 

 

EQ1 contains 3n − 2 unknowns: ai, bi, and ci  for i = 1, 2, … , n − 1 and cn.  We can find bk by applying the zero-order constraint :

                                                

Similarly, we can find the ak by applying the zero-order constraint at the other endpoint:

                                                        

It remains to get a formula for the ck, which, as we’ve shown, also represent the values of the second derivatives of s at the control points.  If we apply the first-order continuity condition   where in each case, some of the terms will be zero and we simplify:

                                    

whence, for 1 < k < n,

                                                    

 

Now, since the formulas for ak and bk both depend in ck, we can substitute to obtain n−2 equations involving only ck-1, ck, and ck+1,  for k = 2, 3, … ,  n − 1

                      

 

If you then impose the natural spline boundary conditions; that is, that the curvature at the extreme endpoints is zero, then

                                                                    

For simplicity, let wk represent the slope

                                                           

so that the equation for ci values can be written as the dot product

                                             

Together with the natural spline boundary constraints, this can be written in matrix form as

Ac = d:

   

Isn’t that impressive?

 

Tomorrow we’ll maybe look into writing out the pseudocode and some c++ to implement this.