Back to December Calendar            ←Previous Entry                             Next Entry→

December 6, 2005

My First Successful Arithmetic Parser!

The purpose of this paper is to describe my first success in creating an arithmetic parsing computeran operator-precedence parser that supports some minimal parsing features such as confix (grouping) operators, function application, and operator name disambiguation by context.  The exclamation point in the title is an expression of my own joy in finally tinkering a way to something that seems to work with a reasonable measure of reliability.  I hope simply seeing how the parsing logic is implemented in c++ code in this way is joy enough for the gentle reader.

Define an expression as a sequence of operators and operands where operators fall into one of the following categories:

The confix and function application operators are parsed using an open symbol and a close symbol. The "open" symbol to the left-hand side and "close" symbol to the right.

Constructing the parser

The expression parser presented here uses a shift/reduce parser (with zero look-ahead) involving two separate stacks: one for operators (opr) and one for operands (val.)  Any operand in the input stream is immediately shifted onto the operand stack; operators are immediately shifted onto the operator stack only if the operator stack is empty. Otherwise, the following table determines the action of the parser depending on the type of the operator on top of the operator stack and on the type of the current operator token.

Parsing table

Description of parsing actions

• A shift operation pushes the current operator token onto the operator stack (and maybe gets the next symbol too.)
• A reduce operation pops the operator token off the top of the operator stack, and then pops the appropriate number of operands from the operand stack: applying the operator to the operand(s) and pushing/replacing the result on the operand stack appropriately. Reduction of confix operators and of function application requires popping two operators (open and close) off the operator stack.  The name of the operation may be another operand.
• A precedence operation (computed by parseTable in the instance presented here) determines the relative precedence of the operator on top of the operator stack (tok) and the current operator (pretok).
• If pretok has a lower precedence than tok, shift.
• If pretok has a higher precedence than tok, reduce.   
• A precedence/associativity operation first compares the precedence according to the precedence operation: if the precedence is equivalent, associativity is considered:
• If top associates left of current, reduce.
• If top associates right of current, shift.

Rejecting Invalid Expresions

Operator-precedence parsers are often avoided because they accept invalid strings. The shift-reduce parser as specified above will consider the expressions x + x, + x x, and x x + equivalent, even though only the first form is correct. This weakness is easily remedied with the use of the following state machine to track what type of operator or operand is expected at any given point in time.

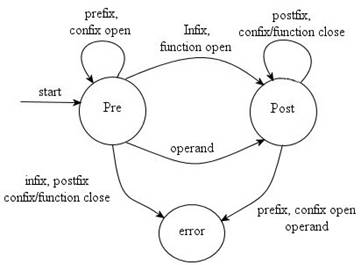
The state machine has three states:

·        the pre-op state where confix open and prefix operators accumulate until an operand arrives, triggering

·        the post-op state where we can accumulate postfix operators to the operand or confix close operators and function close calls.

·        Finally, the error state that will be entered if an invalid parse is detected.

Disambiguation of Operator Names

The meaning of an operator’s token may depend on context. Obvious examples are the unary negation and binary minus operators that use the same symbol ' -',  the absolute-value confix operators use the same symbol '|' for both open and close, and the '+' operator for regular expressions that is both a postfix positive closure operator and an infix operator.

A respectable operator-precedence parser should support such common parsing requirements as function application, confix (grouping) operators, and operator name disambiguation.

An Example

Below is a blow-by-blow accounting of the operator precedence algorithm as it is used to parse the expression a*|b+c|+5^a^b using standard rules for precedence and associativity.