Back to July Calendar	←Previous Entry	Next Entry→
September 23, 2005 Ok, more thoughts on generating functions for partition counting.  Generating functions are, generally, polynomials with ``interesting'' properties. For example, in the polynomial (1 + x)n, the coefficient of xi gives the binomial coefficient, nCi, which is the number of ways of choosing i things from n things if repetition is not allowed and order doesn't matter.  The generating function for the partition function p(n) is given by: P(z) = (1 + z + z2 + . . .)(1 + z2 + z4 + . . .)(1 + z3 + z6 + . . .) . . . The first term in this polynomial represents the number of partitions which have value 1. Similarly, the second term in this polynomial represents the number of partitions which have value 2. So in P(z) the coefficient of zn gives p(n).  P(z) can be simplified in the following way: P(z) = (1 + z + z2 + . . .)(1 + z2 + z4 + . . .)(1 + z3 + z6 + . . .) . . . =  This is essentially just the Euler approach discussed in this slog a few days ago. Young's lattice Defintion:  A Ferrer diagram for a partition λ = (λ1 , λ2 , . . . ,λm ) is an arrangement of rows of dots, all evenly spaced and flush left where the ith row has λi dots.  Dot's nice. We define an order on the partitions in the following way: Given two partitions,  λ = (λ1 , λ2 , . . . ,λm ) and δ = (δ1 , δ2 , . . . , δn ), we say that λ ≥ δ iff m ≥ n and " 1 £ i £ n,  λi ≥ δi.  This can also be viewed in terms of containment in the Ferrer's diagram, as illustrated by the (4,3,2) partition containing the (2,2,2) partition at right. 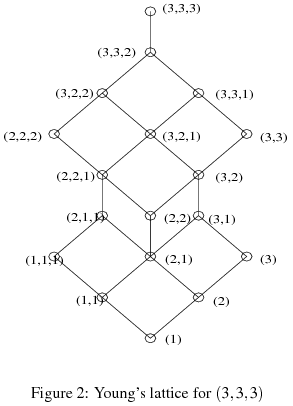Definition:  Given a partition λ, Young's lattice Yλ is the lattice of all partitions less than or equal to λ.  Young's lattice for (3,3,3) is shown at right. Notice that each "level" down is a partition of the number 1 less that the number above.  The third level up includes a complete partition of its rank (3), but above that, only partitions whose number of parts is less than or equal to those in the top node are included, and these are further restricted in that no part can exceed the corresponding part in the top node. Claim:  The number of partitions of n with m parts and no part bigger than k is equal to the number of partitions of n with k parts and no part bigger than m. Proof:  This is easily seen by taking any Ferrer diagram and flipping it so that the top row becomes the left column and vice versa.  The question of how to list partitions and their Ferrer diagrams  for a given integer remains.  How about a slightly larger number for an example listing: N = 10. 10 9-1 8-2 8-1-1 7-3 7-2-1 7-1-1-1 6-4 6-3-1 6-2-2 6-2-1-1 6-1-1-1-1 5-5 5-4-1 5-3-2 5-3-1-1 5-2-2-1 4-4-2 4-4-1-1 4-3-3  1-1-1-1-1-1-1-1-1-1  2-1-1-1-1-1-1-1-1  2-2-1-1-1-1-1-1  3-1-1-1-1-1-1-1  2-2-2-1-1-1-1  3-2-1-1-1-1-1  4-1-1-1-1-1-1  2-2-2-2-1-1  3-2-2-1-1-1  3-3-1-1-1-1  4-2-1-1-1-1  5-1-1-1-1-1  2-2-2-2-2  3-2-2-2-1  3-3-2-1-1  4-2-2-1-1  4-3-1-1-1  3-3-2-2  4-2-2-2  3-3-3-1 5-2-1-1-1  and 4-3-2-1 are symmetric      Thus, in addition to the 20 non-symmetric Ferrer pairs, there are two symmetric ☼☼☼☼☼☼☼☼☼☼ ☼☼☼☼☼☼☼ ☼☼ ☼ ☼☼☼☼☼☼ ☼ ☼ ☼ ☼ ☼☼☼☼☼ ☼☼☼ ☼ ☼ ☼☼☼☼☼☼☼☼☼ ☼ ☼☼☼☼☼☼ ☼☼☼☼ ☼☼☼☼☼ ☼☼☼☼☼ ☼☼☼☼☼ ☼☼ ☼ ☼ ☼ ☼☼☼☼☼☼☼☼ ☼☼ ☼☼☼☼☼☼ ☼☼☼ ☼ ☼☼☼☼☼ ☼☼☼☼☼ ☼☼☼☼ ☼☼☼☼ ☼☼ ☼☼☼☼☼☼☼☼ ☼ ☼ ☼☼☼☼☼☼ ☼☼ ☼☼ ☼☼☼☼☼ ☼☼☼☼ ☼ ☼☼☼☼ ☼☼☼☼ ☼ ☼ ☼☼☼☼☼☼☼ ☼☼☼ ☼☼☼☼☼☼ ☼☼ ☼ ☼ ☼☼☼☼☼ ☼☼☼ ☼☼ ☼☼☼☼ ☼☼☼ ☼☼☼ ☼☼☼☼☼ ☼☼ ☼ ☼ ☼ ☼☼☼☼ ☼☼☼ ☼☼ ☼   Hi mom. Just experimenting with some style sheet stuff here.

http://www.btinternet.com/~se16/js/partitions.htm

http://www.ece.utexas.edu/~garg/

http://www.delphiforfun.org/Programs/Math_Topics/Integer_partitions.htm

http://www.math.mtu.edu/~kreher/cages.html

 

Hi mom.  Just experimenting with some style sheet stuff here.