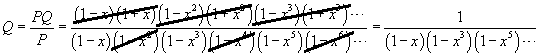Back to July Calendar	←Previous Entry	Next Entry→
September 20, 2005 Does anyone remember Deitel exercise #17.8?  It's humbling that such a lowly numbered exercise in Deitel is causing such grief!  Let's restate the problem: Write a program that inserts 25 random integers from 0 to 100 in order in a linked list object.  You know, if you take the simplest approach to this, you would just create the list in order in the first place, rather than trying to  order it after it's created.  This may simplify the deal a great deal and give a whole new perspective how to deal the deal for this lowly numbered exercise!  Still, you would need a function for inserting the data in the link where it's ordered.  Kreith, K., & Kysh, J. (1988). The fourth way to sample k objects from a collection of n. Mathematics Teacher, 81, 146-149.{T} [sampling problem, replacement and order] Meanwhile, I've been asked to look into the problem of writing a program to compute the partitions of an integer.  For example,  there are 10 non-trivial partitions of 6: 5,1 4,2 3,3 4,1,1 3,2,1 2,2,2 3,1,1,1 2,2,1,1 2,1,1,1,1 1,1,1,1,1,1 I like Ask Dr. Math, so I'll start with his inexplication of this problem solution I will use the notation P(n,p) to represent the partition of n into p parts, for example P(50,10) is number of partitions of 50 into 10 parts. One example is (1,2,2,3,4,5,6,7,9,11). There is a recurrence relationship which allows you to fill in a table of values. So if you have the patience you can complete a table to get the answer you want. The recurrence relationship is P(n,p) = P(n-1,p-1) + P(n-p,p) And if this is applied continuously we get: P(n,p) = P(n-p,1) + P(n-p,2) + P(n-p,3) + .... + P(n-p,p) So for example: P(20,5) = P(15,1) + P(15,2) + P(15,3) + P(15,4) + P(15,5) = 1 + 7 + 19 + 27 + 30 = 84 Below is the start of such a table: n|1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 -+-------------------------------------------------------------------- p| 1|1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2| 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9 10 3| 1 1 2 3 4 5 7 8 10 12 14 16 19 21 24 27 30 33 4| 1 1 2 3 5 6 9 11 15 18 23 27 34 39 47 54 64 5| 1 1 2 3 5 7 10 13 18 23 30 37 47 57 70 84 6| 1 1 2 3 5 7 11 14 20 26 35 44 58 71 90 7| 1 1 2 3 5 7 11 15 21 28 38 49 65 82 8| 1 1 2 3 5 7 11 15 22 29 40 52 70 9| 1 1 2 3 5 7 11 15 22 30 41 54 10| 1 1 2 3 5 7 11 15 22 30 42 If you require P(50,10) you should take the table as far as the n = 40 column, and then find: P(50,10) = P(40,1) + P(40,2) + P(40,3) + ..... + P(40,10) http://www.csse.monash.edu.au/~lloyd/tildeAlgDS/Recn/Partition/?inp=7&opt= - Doctor Anthony, The Math Forum http://mathforum.org/dr.math/ Dr. Math (who has a mater's degree in...math!) seems to have made some errors above...for instance P(7,3) = 8 since claims without justification that  P(n,k) = P(n-1,k-1) + P(n-k,k) but how do we justify this? Let f(n) be the total number of partitions of n (that is, the number of ways to write n as a sum of natural numbers.)  Then f(n) = P(n,n) where P(n,k) can be found recursively by considering that P(1,k) = P(n,1) = 1 for all k and n. P(n,k) = P(n,n) anytime k >= n P(n,n) = 1 + P(n,n–1) Computing the Partitions of n  There are, in fact, many different ways of determining the number of partitions f(n) of a given integer n.  Euler responded to the partition question (as posed by Phiippe Naudé) by producing, in his Eulerian fashion, the generating function wherein the coefficient of xn in the expansion is none other than f(n).  How can this be, and what made Euler think of it?  Well, Euler had a gift for counting.  In fact, he counted subsets of these partitions such as those having all distinct summands and those with only odd summands. Actually listing out the partitions and counting them that way is not practical since even small inputs have huge outputs, such as f(24) = 1575.  Euler was deep in the milieu of infinite series expansions, so he expressed the following product: Q = (1+x)(1+x2)(1+x3)(1+x4)(1+x5)(1+x6)... Expanding, one arrives at 1 + x +x2 + 2x3 + 2x4 + 3x5 + 4x6 + 5x7 + 6x8 + 8x9 + 10x10 + ... To get some idea of how these coefficients are formulated, consider the coefficient of x6. There are 4 ways to get a product of x6: 1·1·1···1·x6,    1·1·1···1·x·x5,   1·1·1···1·x2·x4,   1·1·1···1·x·x2·x3, and these correspond directly to the number of partitions of 6 into distinct integers: 6,   1+5,   2+4.   1+2+3 Now, recall the geometric series expansion and by implication, Thus, is an infinite product of infinite series.  Jawheeze!  Multiplying it out you get the same terms as we did above 1 + x +x2 + 2x3 + 2x4 + 3x5 + 4x6 + 5x7 + 6x8 + 8x9 + 10x10 + ... =1 + x+ x1+1 + (x1+1+1 + x3) + (x3+1+ x1+1+1+1) + (x5+ x3+1+1+ x1+1+1+1+1) + (x5+1 + x3+3 + x3+1+1+1 + x1+1+1+1+1+1) + ... but now, the interpretation is that each coefficient is the number of ways that term's degree can be written as a sum of odd integers.  This led Euler the Leonhard to the theorem: Theorem:  The number of different ways to partition an integer as a sum of distinct natural numbers is equal to the number of ways that integer can be partitioned as a sum of odd naturals. Proof:  Let Q = (1+x)(1+x2)(1+x3)(1+x4)(1+x5)(1+x6)... , as above.  Now consider the product of sort of 'conjugate' factors, P = (1–x)(1–x2)(1–x3)(1–x4)(1–x5)(1–x6)... .  Observe that every other factor is a difference of squares, such as 1–x2 = (1–x)(1+x), 1–x4 = (1–x2)(1+x2), and so on, so that, in fact, every factor of Q appears is also a factor of P.  Thus can we write the reciprocal of Q as which proves it!  While this proof clearly shows the genius of Euler, it is a far stretch from the recursive approach I started with.  More on that tomorrow? Later, I want to remember to look at www.theory.csc.uvic.ca/~ca/gen/nump.html   http://www.research.att.com/cgi-bin/access.cgi/as/njas/sequences/eisA.cgi?Anum=A000041 http://www.research.att.com/~njas/sequences/Sindx_Par.html