September 07, 2005
I skimmed chapter 2 of the Grune/Jacobs book: rough sledding in the realm of formal-linguistics and generating sentences according to somewhat arbitrary and abstract rules of abstract grammars. So I skip on to chapter 3, which is titled, Introduction to Parsing. It begins with this fairly concise definition of parsing:
To parse a string according to a grammar means to reconstruct the production tree (or trees) that indicate how the given string can be produced from the given grammar.
With the 12 grammar rules:
1. SumS → Digit { A0:=A1 }
2. Sum → Sum + Sum { A0:=A1+A3 }
3a. Digit → 0 { A0:=0 }
.......
3j. Digit → 9 { A0:=9 }
3+5+1 is described a spuriously ambiguous because
it can be parsed in several different ways:
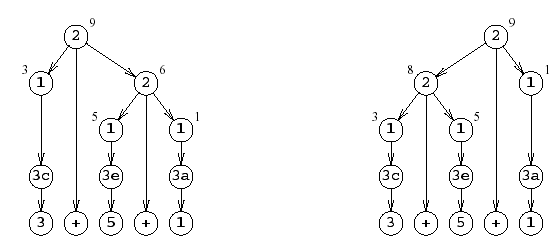
So rule 1 says that Sum can be a digit (rules 3a,3b,...,3j for digits 0,1,2,...,9) and rule 2 says that Sum can also be the result of adding two digits. It is ambiguous which two digits to add together first, but since it doesn't ultimately affect the final result, it's a spurious ambiguity. Of course, if Sum were replaced by Difference, the ambiguity would be essential. This illustrates the associativity of + and the lack of associativity of –.
While the tree is very pretty, it a bit gangling. To avoid big production trees, linearization methods are developed, such as the prefix method, which for the right tree above simply lays out the left most node starting at the top: 2 2 1 3c 1 3e 1 3a. The postfix method lists rules of left-most nodes in a bottom up fashion, leading to this representation of the same tree as: 3c 1 3e 1 2 3a 1 2.
Finally, the infix method, grouping symbols are used to indicate the hierarchy of the same tree like so: (((3c)1) 2 ((3e)1)) 2 ((3a)1).
Again, I spent a long time speed glancing over formal-linguistic stuff until I got to section 9.1 where we encounter the mathematical expression 4 + 5 * 6 + 8, for which Gruner/Jacobs suggest the shift/reduce parsing algorithm which is loosely described in terms of finding "the handle," which in this case starts out being 5*6 and then using it to reduce to, in this case, 4 + 30 + 8. The handle is then 4+30 and finally 34+8, leading to the semantic value 42...the answer!
G/J then suggest a very simple grammar for simple arithmetic expressions:
SS → # E #
E → E + T
E → T
T → T * F
T → F
F → n
F → ( E )
Here, "S is the start symbol, E stands for “expression”, T for “term”, F for “factor” and n for any number. The last causes no problems, since the exact value of the number is immaterial to the parsing process. We have demarcated the beginning and the end of the expression with # marks; the blank space that normally surrounds a formula is not good enough for automatic processing. This also simplifies the stop criterion: the parser accepts the input as correct and stops when the terminating # is shifted, or upon the subsequent reduce."
Fully parenthesized grammar has expressions
SS → # E #
E → ( E + T )
E → T
T → ( T * F )
T → F
F → n
F → ( E )
where each operator
together with its operands has parentheses around it. Such expressions
are generated by the grammar of
Figure 9.3. Our example expression would have the form
# ( ( 4 + ( 5 * 6 ) ) + 8 ) #
Now finding the handle is trivial: go to the first
closing parenthesis and then back to the nearest opening parenthesis.
The segment between and including the parentheses is the handle. Reduce
it and repeat the process as often as required. Note that after the
reduction there is no need to start all over again, looking for the
first closing parenthesis: there cannot be any closing parenthesis on
the left of the reduction spot, so we can start searching right where we
are. In the above example we find the next right parenthesis
immediately and do the next reduction:
# ( ( 4 + 30 ) + 8 ) #