August 23, 2005
It's the simplest things that make for the richest complexity.
Let's compare the DDA and Bresenham algorithms for line rasterization. Here's a magnification of one triangle drawn with yesterdays code:
| Each of the triangle's edges are first drawn in black
with the DDA algorithm and then over drawn with either red
(if not a steep line) or blue (if steep.) So, here's
how this came to be: from the lower left vertex to the right
vertex, a black rasterization of the line using DDA is
drawn, then it is (sort of) duplicated with the red
Bresenham rasterization. Similarly for the next two
edges proceeding counterclockwise around the triangle.
By outputting data to the console window (for some strange reason, I'm using "printf" instead of "cout") we can numerically analyze the results of this experiment and try to make sense of these in terms of the pixels plotted, as evidenced in the picture. |
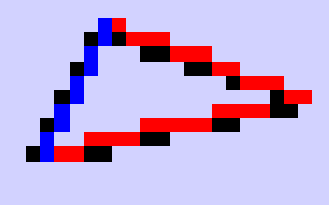 |
What this means is that the black pixels may or may not be overwritten by the red/blue pixels.
The vertices (by happenstance) turn out to have coordinates (5,5), (23,9) and (9,14).
Thus, for the first (bottom) edge, we have Δy=4 and Δx=18. The diagram is cropped so it doesn't look like it, but the big black pixel on the lower left, would have been at (5,5). Then it would have been painted red, then black again, and then...blue? Why isn't it blue? Hmmm....
| x | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| y | 5 | 5 | 5 | 6 | 6 | 6 | 6 | 7 | 7 | 7 | 7 | 7 | 8 | 8 | 8 | 8 | 9 | 9 | 9 |
| error | 4 | 8 | 12 | -2 | 2 | 6 | 10 | -4 | 0 | 4 | 8 | 12 | -2 | 2 | 6 | 10 | -4 | 0 |
As for the black pixels, that's the DDA algorithm, so let's look at it, too. The slope is 2/9 = 0.22222... So, as the table below indicates, you should get exactly the same values with the rounding that you got with Bresenham. This causes me to realize that I have a mistake: the (int)x expression doesn't round x, it truncates it!
| x | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| y | 5 | [5.2] | [5.4] | [5.6] | [5.8] | [6.1] | [6.3] | [6.55] | [6.7] | [6.99] | [7.2] | [7.4] | [7.6] | [7.8] | [8.1] | [8.3] | [8.55] | [8.7] | 9 |
So I add a round function:
int round(float x) {
if (x-(int)x < 0.5) return (int)x;
else return (int)(x+1);
}
and there are no more black pixels!
How about the fill routine? Tomorrow.