|
December
1, 2005
Back to Bernstein Globs
Some
account of my activities in this area must be at least summarized, given the
flurry of activity that engendered. I
partnered mostly with Bill Bernstein, one of the Bernstein brothers who
hatched the idea of globs. If this is
the first you’ve heard of this, or you’d like to review what they are, go
back to here.
To be sure,
the basic definitions bare repeating:
Bernstein globs are dissections of a connected planar region
whose boundary is a simple closed curve (loosely, think circle, or pizza pie)
into connected sub-regions, which are homogeneous image areas called blobs,
each a with simple closed curve boundary and containing at least one non-zero
length of the glob's boundary.
A glob is an amalgam of blobs such that no blob is
"land-locked." That is, each blob contains some non-zero
length the glob's circumference. Two globs are equivalent if one can be
transformed into the other by moving its blob's borders without crossing and
while preserving instances of glob/blob border intersections.
The genus of a glob is the number of blobs it
contains.
|
Some of
the questions we’ve asked about the globs:
·
How to represent them?
·
How to tell if two globs are different?
What might a canonical representation be?
·
How are globs related to the Catalan
numbers?
·
One of the overarching goals of the glob
project was to count the number of globs for each genus and keep advancing
the sequence. A tentative tabulation
is shown at right.
·
Can we write code to draw a glob?
|
|
Genus
|
Number
of globs
|
|
1
|
1
|
|
2
|
1
|
|
3
|
2
|
|
4
|
4
|
|
5
|
9
|
|
6
|
23
|
|
7
|
69
|
|
8
|
230
|
|
9
|
877
|
|
10
|
3595
|
|
11
|
15706
|
|
12
|
71391
|
|
13
|
?
|
|
How to Represent Globs
The
two main ways to represent the globs are graphical and syntactical. For instance,
a graphical representation
of the 6-glob (formed of 6 blobs) with syntactical representation 1((1/1/1)) is shown at left below. More bigger by far is 1(((((1))1/1/(11)/(1/1)/(1(1))/(1/1)))), the
syntactical representation of the 23-glob whose graphical representation is shown
at right, over a zebra pattern! I hope
no one will protest that the big 7-blob in the midst of this 23-glob is a
two-tone blue bleed and thus not entirely a “homogeneous image area,” as the
definition requires. I got carried
away…
You’ll want
to read my slog on drawing
Bernstein globs to grasp this, but I will give a brief account of how I
use MatLab to draw globs. The m-file I wrote is here:
function drawGlob01(n, arcs)
hold on;
% uncomment
these lines if you want to see the unit circle
%
t1=0:.05:2*pi;
%
plot(cos(t1),sin(t1));
% The first
part draws all n nubs equally distributed outside the unit circle
for i = 0:n-1
t=2*pi*(i/n-.25):.002:2*pi*((i+1)/n+.25);
x=(sin(2*pi*(i+1)/n)-sin(2*pi*i/n)+(1-cos(2*pi/n)).*cos(t))/sin(2*pi/n);
y=(cos(2*pi*i/n)-cos(2*pi*(i+1)/n)+(1-cos(2*pi/n)).*sin(t))/sin(2*pi/n);
plot(x,y,'k','LineWidth',2);
end;
% The second
part uses the matrix tabulating index pairs for each interior
% arc
connection. This tells us how to
defined the t domain and what
% angles to
pass to the x and y parameterization functions.
for i = 1:size(arcs,1)
t=2*pi*(arcs(i,2)/n+.25):.01:2*pi*(arcs(i,1)/n+.75);
x=(sin(2*pi*arcs(i,2)/n)-sin(2*pi*arcs(i,1)/n)+(1-cos(2*pi*(arcs(i,2)-
arcs(i,1))/n)).*cos(t))/sin(2*pi*(arcs(i,2)-arcs(i,1))/n);
y=(cos(2*pi*arcs(i,1)/n)-cos(2*pi*arcs(i,2)/n)+(1-cos(2*pi*(arcs(i,2)-
arcs(i,1))/n)).*sin(t))/sin(2*pi*(arcs(i,2)-arcs(i,1))/n);
plot(x,y,'k','LineWidth',2);
end;
The
parameter n can be any positive
number greater than the number of rows in arcs, and arcs needs to be spelled
out properly to produce the glob. The
globs used above have, respectively, the index lists:
>> arcs'
ans =
8
2 4 6
9
11
3 5 7
0
and
>> arcs2'
ans =
Columns 1 through 13
1
2 3 7
7 8 9
12 14 16
17 17 18
6
5 4 12
13 11 10
13 15 20
19 18 19
Columns 14 through 26
21
22 24 27
28 28 29
30 34 35
37 37 38
26
23 25 33
32 29 32
31 40 36
39 38 39
Thus the
first glob shown above is created by
The n vertices evenly distributed around
unit circle are numbered 0, 1, 2, … n
– 1 and is vertex j is connected to
vertex k then we include j, k
in the matrix of index pairs. It’s ok
if you use an index greater than n,
such as the first pair in the first glob above: 8, 11. I use 11 instead of 1=11mod(10) because
it works better in the m-file.
How Can You Tell Whether or Not Two Globs are the Same?
The graphical
glob representations developed here require each blob to intersecting the
unit circle orthogonally in circular arcs contained inside the unit
circle. In these diagrams, little
circular arcs are also placed regularly around the outside circumference so
the boundaries will meet 1st order continuity conditions. This is mostly for aesthetic appeal. Most lovely and blobish, I think.
Thus, if
two globs are the same, then it seems reasonable that one can be obtained
from the other by some combination of rotation and flip. This sort of requires a human observer,
however. The syntactical
representation is formed by starting with any 1-blob (there is at least one)
wrte a “1” and, reading around the perimeter counterclockwise, follow these
rules:
- If the next blob
encountered is a 1-blob, write a "1".
- If the next n-blob
has n > 1 and has not been encountered before, write a
"(".
- If the next n-blob
has been encountered before and will be encountered again, write a
"/".
- If the next n-blob
has been encountered before and will not be encountered again, write a
")".
Thus, if
you start at the green 1-blob on the right of the 6-glob above you get the
representation 1((1/1/1)) if but starting at the next 1-blobs you’d
get equivalent representations 1(1/1/(1)) or
1(1/(1)/1) or 1((1)/1/1). To choose amongst these, we assigned
a numerical value to each symbol, ‘1’=1,
‘(’=2, ‘/’=3 and ‘)’=4. The
equivalent representation are then ordered from highest to lowest numerical
value (most significant digit to the left.)
For instance, among the 4 representations of the 6-glob we have
1(1/1/(1))=1213132144
1(1/(1)/1)=1213214314
1((1/1/1))=1221313144
1((1)/1/1)=1221341414
So the
first one (the lowest numerical value) is considered the canonical form, and
is then a unique syntactical representation for the glob.
Perhaps
this is a good point of entry into the globGenerator
program. But, first let’s examine the xlate function. This purpose of this program is to take one
glob syntax and translate it to the equivalent syntax from the point of view
of some other 1-blob. It inputs a vector of char, vChar
and the index i of the 1-blob
whose perspective we seek and outputs the vector
of char, vXlate, with that perspective. For instance xlate(“1((1)/1/1)”,vXlate,6)
outputs vXlate=1(1/1/(1)).
This piece
was designed and written almost entirely by Bill Bernstein, I’ve edited some
comments.
|
/* 'xlate' Translates
string 'vChar' from the perspective of the '1' in position i.
The string
is translated from the innermost set of containing parenthesis out.
Indices 'r_ndx'
and 'l_ndx' move right and left away from i.
The state variable 'ss' tells if you:
0 - have not yet hit a slash or containing paren,
1 - have hit a slash (so must cont. to
containing paren), or
2 - have hit the containing paren and
are done with current side of loop.
Booleans 'ldone'
and 'rdone' tell when the left or right end of the string has been reached.
*/
void xlate(vector<char> &vChar, vector<char> &vXlate, int
i) {
int l_ndx,
r_ndx, j, k, max = vChar.size() - 1,
ss, dzp; // ss is the
state variable, dzp is for “dead zone parameter”
bool rdone = 0, ldone = 0;
vector<char>
vNew;
char
x;
vNew.clear(); vXlate.clear();
for (j
= 0; j <= max; ++j) {
vXlate.push_back('0'); // Load both with zeros up to vChar.size()
vNew.push_back('0'); }
vNew[0] = '1'; vNew[i] = '1'; // We know
there are 1’s at 0 and i
if (i
== max) rdone = 1; // No need to search past the end.
else r_ndx
= i + 1;
if (i
== 1) ldone = 1; // No need to search past the
beginning.
else l_ndx
= i - 1;
do { // big loop
if
(!rdone) { //
Do right search
ss = 0; // Haven’t hit
a ‘/’ or a ‘)’ yet
do
{ // right
side
switch
(vChar[r_ndx]) {
case '1':
vNew[r_ndx] =
'1'; // 1’s are always preserved
if (r_ndx == max) rdone = 1;
else ++r_ndx;
break;
case '(': // a '(' going rt means there is a dead zone
vNew[r_ndx] =
'('; // preserve the container…
dzp = 1;
do {
++r_ndx;
vNew[r_ndx] =
vChar[r_ndx]; // …and its contents
if
(vChar[r_ndx] == '(') ++dzp; // deeper into the
dz
if (vChar[r_ndx] == ')') --dzp; // crawling out of dz
} while (dzp > 0);
if (r_ndx == max) rdone = 1;
else
++r_ndx;
break;
case '/':
if (ss == 0) { // If
you hit the first slash,
vNew[r_ndx] =
'('; //
change it to a ‘(‘
ss = 1; } // Change state
to indicate slash hit.
else vNew[r_ndx] = '/'; //
Else, slashes preserved
++r_ndx;
break;
case ')': // If no ‘/’ or ‘)’ yet
if (ss == 0) vNew[r_ndx] = '('; //reverse ‘)’ to ‘(‘
else vNew[r_ndx] = '/'; //else
replace ‘)’ with ‘/’
ss = 2; //and set
state to done
if (r_ndx == max) rdone = 1; //maybe before
actually
else ++r_ndx; //reaching
the end
break;
} // endswitch
} while
((ss < 2) && (!rdone)); // ss==2 is the bail condition
}
//endif
if
(!ldone) {
ss = 0;
do
{ // left
side – like the right side, only opposite…
switch
(vChar[l_ndx]) {
case
'1':
vNew[l_ndx] =
vChar[l_ndx];
if (l_ndx == 1) ldone = 1;
if (l_ndx == 0) ldone = 1;
else --l_ndx;
break;
case ')':
vNew[l_ndx] =
')';
dzp = 1;
do {
--l_ndx;
vNew[l_ndx]
= vChar[l_ndx];
if (vChar[l_ndx] == ')') ++dzp;
if (vChar[l_ndx] == '(') --dzp;
} while (dzp > 0);
if (l_ndx == 1) ldone = 1;
else --l_ndx;
break;
case '/':
if (ss == 0) {
vNew[l_ndx] =
')';
ss = 1; }
else
vNew[l_ndx] = '/';
--l_ndx;
break;
case '(':
if (ss == 0) vNew[l_ndx] = ')';
else vNew[l_ndx] = '/';
ss = 2;
if(l_ndx == 1) ldone = 1;
else --l_ndx;
break;
} // end switch
} while
((ss < 2) && (!ldone));
}
// endif
} while
((!ldone) || (!rdone));
for (k
= 0; k <= max; ++k)
vXlate[k]= vNew[(k+i)% (max+1)]; // Rotate the 1 at i to front
}
|
Now
that we have a way to, given a glob syntax, find all equivalent
representations, we have the getCanForm()
function sort through them for the unique one whose numerical value is
least. The conv2nums function switches from the glob syntax to an
array of numbers that will be well-ordered in an obvious way. The getLower()
function replaces vlownum with
vNums if vNums is lower. The function getRevGlob()
is aptly named: it simply produces the syntax for the equivalent glob, only
flipped. Since these are equivalent
globs, we have to check them too. This was also written almost entirely by
Bill Bernstein.
|
//
'getCanForm' takes the input string 'vChar' and returns its 'canonical
form,'
// e.g. the
lowest number of all the xlate strings and their reversals that can
// be made
from all the '1's in vchar. All
strings are converted to numerical form
// first:
'1' = 1, '(' = 2, '/' = 3, ')' = 4.
void getCanForm(vector<char> &vChar, vector<char> &vlownum) {
int i
= 1; char z;
vector<char>
vCharRev, vNums, vXlate;
vXlate.clear(); vCharRev.clear();
vNums.clear(); vlownum.clear();
//
initialize vlownum to be the same size as vChar, and all 5’s
for (int j=0; j < vChar.size(); ++j)
vlownum.push_back('5');
conv2nums(vChar, vNums);
getLower(vNums, vlownum);
getRevGlob(vChar, vCharRev);
conv2nums(vCharRev, vNums);
getLower(vNums, vlownum);
while
(i < vChar.size()) {
if
(vChar[i] == '1') {
xlate(vChar, vXlate, i);
conv2nums(vXlate, vNums);
getLower(vNums, vlownum);
getRevBlob(vXlate,
vCharRev);
conv2nums(vCharRev, vNums);
getLower(vNums, vlownum);
}
++i;
}
}
|
In earlier
approaches to counting, we generated random n-globs and added new ones to a
growing list until it seemed that no new ones would be found and so the list
should be complete; essentially the same Monte Carlo
approach as was used in the necklace paper.
The approach here is to generate a big list that is sure to contain
all n-globs and then prune it down to just the unique ones. The comparison of over-generate and cull
vs. guess and check approaches is interesting, but, for now, I’ll just give the over-generate and cull
approach.
It turns out that n-glob numbers are closely related to
Catalan numbers, which will not be surprising to Catalan afficianados.
A Catalan
number can be defined by the formula
For
instance, .
These
numbers count a wide variety of different construct types, including the
number of ways of legally nesting n pairs of parentheses: that is, for every
open, you must have a close, and the can be no new close that doesn’t match a
previous open. Thus C2 = 2; namely, (())
and ()(). For ways of mixing 3 pairs we can list
()()(),
()(()),
(())(),
(()())
and ((())).
The
connection to glob syntax become more evident when you substitute a 1 for
each empty pair of adjacent open/close parentheses: 1=(). This is, in a
way, like using the null set symbol for the empty set: Ø = {}: a single
symbol to represent a pairing of empty grouping symbols. Thus, the 5 possible
strings of 3 legally interleafed pairs can be listed as
111,
1(1), (1)1 (11) and ((1)).
In fact, as
is, only 2 of these are distinct 3-globs: 111 and 1(1), but we haven’t
introduced the ‘/’ yet. The plan is to
produce a mass Catalan parenthetical interleaves which we can surely cull and
slash to produce a complete list of unique n-globs, thus enumerating them.
Now, if we
make the assumption that we always start from a 1-blob in forming the syntactical
representation then we can gain specificity without loss of generality by
noting that every 4-glob can be culled from a list obtained by appending a
‘1’ to the front of each of the 5 strings above, producing, 1111, 11(1),
1(1)1, 1(11) and 1((1)) and then adding slashes. In particular, 1(1/1) will distinguish
1(11) from 11(1), which can’t take a slash.
Since I’m
more of a coordinate oriented guy than a parsing partisan, I like the
equivalent representation of Catalan numbers as the number of lattice paths
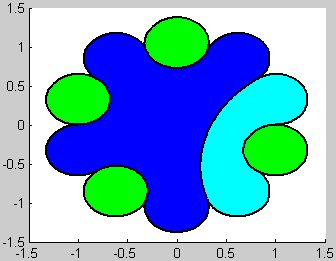
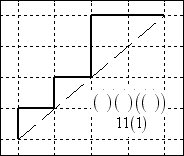
from (0,0) to (n,n) which never venture below the diagonal. (Note: if you rotate these 45 clockwise you
get a kind of mountain-looking diagram. This is often how these are referred
to in the literature, such as Richard Guy’s The Second Strong Law of Small Numbers inVol. 63, No. 1 February
1990 edition of the Mathematics Magazine, or here.)
In these lattice paths, going up opens a
parenthesis pair and going right closes one.
Every such path is then an open/close combination which meets the
condition that no new close not matching a previous open. Thus each of the Catalan parenthetical stings
is also a path on this grid from (0,0) to (n,n) not passing below the
diagonal.
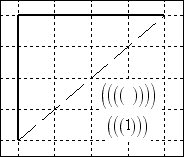
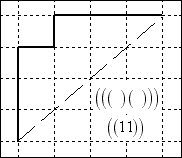
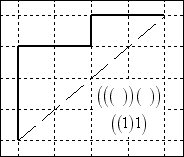
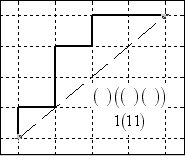
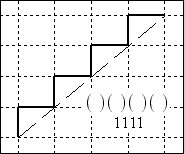
Below is a
sampling of 6 of the 14 such paths from (0,0) to (4,4). The pure parenthetical expression is given,
together with the () = 1 equivalent expression
below the diagonal in each diagram.
What LoadTable() does is tweak this
lattice path idea for creating Catalan parenthetical expressions to create a
table of all possible legal n-glob syntaxes, for a given n—including the
slashes! Starting the first n-glob
with “1(” at coordinates (0,1) on the lattice, each time we’re at a junction in the lattice
where we have a choice of going up or right, an additional glob is created (vector of char is pushed on the stack of vectors named table.)
On one vector a ‘(’ is pushed and on the other, a ‘)’, if the current vector ends with ‘1’ or a ‘)’
or, if it ends with a ‘(’ that
character is replaced by a ‘1’. Anytime a slash can be inserted (after a ‘1’ or a ‘)’,)
a new vector of char is added to the table for that
glob, though this doesn’t affect the path, so the coordinates for that glob
will be the same as the coordinates of the glob it copies. All the while, we keep track of the current
coordinates of each path with integer vectors v_x
and x_y. The current coordinates of the path of the
ith glob is stored in v_x(i),
v_y(i).
Of course,
when the path reaches either the top or the diagonal boundary, there is no
branching.
One aspect
of this I like is that the index of the for
loop goes from 0 to table.size(),
and that table.size() grows
inside the loop. Anyroad, here it is:
|
void
LoadTable(vector<vector<char> >
&table, int n) {
char ch;
vector<char>
vChar;
vChar.push_back('1');
vChar.push_back('(');
vector<int>
v_x;
vector<int>
v_y;
v_x.clear();
v_y.clear();
table.clear();
// initialize
coordinates
v_x.push_back(0);
v_y.push_back(1);
table.push_back(vChar);
bool
done = 0;
while(!done)
{
done = 1; // assume all
are done until you find otherwise
for(unsigned int i =
0;i < table.size(); ++i) {
if(v_x[i]
< n) { // x coord not yet on rt side of box,
done = 0; // so we're
not done yet!
if(v_y[i]
< n) { //
below the top
if(v_x[i]
== v_y[i]) { // on the diagonal so move up
// on the
diagonal parens are balanced and no slashes occur
v_y[i] += 1;
table[i].push_back('('); //move up
}
else
{ // below top and left of diagonal AND LAST MOVE
UP
if(table[i].back() == '(')
{ //make
new glob a
vector<char> newVChar(table[i]); //copy of current
table[i].push_back('('); // go up in current glob
v_y[i]
+= 1;
// go right in new
glob – note replacing ‘(‘ with ‘1’
newVChar.back() = '1';
table.push_back(newVChar); //add new glob
to table
v_x.push_back(v_x[i]+1); //set appropriate
coords
v_y.push_back(v_y[i]-1); //for the new
glob
}
//interior & LAST
MOVE RIGHT...but not on diagonal
if(table[i].back()
== ')') {
vector<char>
newVChar(table[i]);
table[i].push_back('('); //move up
v_y[i]
+= 1;
newVChar.push_back('/');
//move up with slash
newVChar.push_back('(');
table.push_back(newVChar);
v_x.push_back(v_x[i]);
v_y.push_back(v_y[i]);
newVChar.pop_back();
//move right
newVChar.back()
=')';
table.push_back(newVChar);
v_x.push_back(v_x[i]+1);
v_y.push_back(v_y[i]-1);
}
if(table[i].back()
== '1') {
vector<char> newVChar(table[i]);
table[i].push_back('('); //move up-no
slash
v_y[i] += 1;
newVChar.push_back('/');
//move up with slash`
newVChar.push_back('(');
table.push_back(newVChar);
v_x.push_back(v_x[i]);
v_y.push_back(v_y[i]);
// move right
newVChar.pop_back(); // move
right-no slash
newVChar.back()
= ')';
table.push_back(newVChar);
v_x.push_back(v_x[i]+1);
v_y.push_back(v_y[i]-1);
}
} //
end else
}
else
{ //y_n = n so at the top
if
(table[i].back() == '(') {
table[i].back() = '1';
v_x[i] += 1;
}
else {
table[i].push_back(')');
v_x[i] += 1;
}
} //
end else
} // end
if
}
//end for
} // end while
}
|
With slight
modification, you can run this as a stand-alone application. Here’s what the console might look like:
|
How many
parentheses do you want to balance? 5
There are
22 words, and here they are:
1(((1)))
11((1))
1(1(1))
111(1)
1(1/(1))
1(1)(1)
1(1/11)
1(1/1/1)
1(1/1)1
1((11))
11(11)
1(111)
11111
1(1)11
1((1/1))
1((1)1)
11(1/1)
11(1)1
1(11/1)
1(11)1
1((1)/1)
1((1))1
|
There are
obvious redundancies here, there are, after all, only 9 distinct 5-globs. So
the list needs to be culled.
But, since
it contains all possible combinations of characters to comprise a 5-glob
syntax, it should be complete.
One more thing
before the main: Bill’s updateList(),
which he has been so kind as to document with admirable thoroughness, so I
present it as is:
|
//
updateList takes the input string 'lownum' and checks it against
// the list
'cforms'. First, if the list is
empty, is pushes lownum.
// Next it
checks to see if lownum is greater than the last item on the list, in
// which
case it pushes lownum onto the end.
If not, the iterator cfIt steps
// through
cforms until it finds an entry not less than lownum. If this entry is
// greater
than lownum then lownum is inserted into cforms at that spot. If not
// then they
must be equal and nothing is done.
void
updateList(vector<vector<char>
> &cforms,
vector<char> &vlownum, int
reset) {
char
z;
vector<vector<char> >::iterator cfIt = cforms.begin();
reset = 0;
if
(cforms.size() == 0) cforms.push_back(vlownum);
else if(vlownum > *(cforms.end()-1))
cforms.push_back(vlownum);
else {
while
((vlownum > *cfIt) && (cfIt != cforms.end())) ++cfIt;
if
(vlownum < *cfIt) {
cforms.insert(cfIt, 1, vlownum);
reset = 1;
}
}
}
|
At last,
main. Bill added a feature that allows
you to choose whether or not you want to output the globs to text file, globs.txt, which you can toggle by
asking for 0 globs at the prompt. The
first order of serious business in the infinite loop is to create table,
which then needs to be culled by the combination of getCanForm() and updateList().
|
int main() {
int
b_ndx, ii = 0, i, j, reset = 0, entry, guess, writeflag = 0;
char
xx;
vector<char>
vChar, vStrng, vlownum;
vector<vector<char> > cforms, table;
// open a
file for writing
ofstream outGlob("globs.txt",
ios::out);
if(!outGlob)
{
cerr <<
"\ndoh!" << endl;
exit(1);
}
while(1)
{
cforms.clear();
entry = 0;
while
(entry == 0) {
cout << endl <<
endl << "\nEnter number of regions: ";
cin >> entry;
if
(entry == 0) {
writeflag = !writeflag;
if
(writeflag) cout << endl << "File-writing turned on"
<< endl;
else
cout << endl << "File-writing turned off" << endl;
}
}
b_ndx = entry - 1;
ii = 0;
LoadTable(table, b_ndx);
while
(ii < table.size()) {
vChar = table[ii];
getCanForm(vChar, vlownum);
updateList(cforms, vlownum,
reset);
++ii;
}
j = 0;
if
(writeflag) outBlob << "\nWith index " << entry
<< " and " << guess <<
" guesses, found
" << cforms.size() << " blobs: " << endl
<< endl;
cout << endl;
do
{
conv2strng(cforms[j], vStrng);
if
(j<9) cout << " " << j+1 << ". ";
else
cout << j+1 << ".
";
printVector(vStrng); cout
<< endl;
if
(writeflag) writeVector(outGlob, vStrng);
++j;
} while
(j < cforms.size());
}
}
|
Pretty
slick? I don’t know. There’s plenty of room for improvement
through greater efficiencies, but it achieves the objective, which was to
find an over-produce and cull approach to compare with the guess and check
approach to generating a complete list of n-globs.
Here’s a
sampling of output. Note that the
globs come out in order and are numbered:
|
Enter number of regions: 5
1.
1 1 1 1 1
2.
1 1 1 ( 1 )
3.
1 1 ( 1 1 )
4.
1 1 ( 1 / 1 )
5.
1 1 ( ( 1 ) )
6.
1 ( 1 ( 1 ) )
7.
1 ( 1 / 1 / 1 )
8.
1 ( 1 / ( 1 ) )
9.
1 ( ( ( 1 ) ) )
Enter number of regions: 6
1.
1 1 1 1 1 1
2.
1 1 1 1 ( 1 )
3.
1 1 1 ( 1 1 )
4.
1 1 1 ( 1 / 1 )
5.
1 1 1 ( ( 1 ) )
6.
1 1 ( 1 1 / 1 )
7.
1 1 ( 1 ( 1 ) )
8.
1 1 ( 1 / 1 / 1 )
9.
1 1 ( 1 / ( 1 ) )
10. 1 1 ( 1 ) ( 1 )
11. 1 1 ( ( 1 1 ) )
12. 1 1 ( ( 1 / 1 ) )
13. 1 1 ( ( ( 1 ) ) )
14. 1 ( 1 ( 1 / 1 ) )
15. 1 ( 1 ( 1 ) 1 )
16. 1 ( 1 ( ( 1 ) ) )
17. 1 ( 1 / 1 / 1 / 1 )
18. 1 ( 1 / 1 / ( 1 ) )
19. 1 ( 1 / ( 1 / 1 ) )
20. 1 ( 1 / ( ( 1 ) ) )
21. 1 ( ( 1 / ( 1 ) ) )
22. 1 ( ( 1 ) ( 1 ) )
23. 1 ( ( ( ( 1 ) ) ) )
|
|