Math 2A  Chapter 13 Test  Fall 07.                      Name______________________________

Show your work for credit.  Write all responses on separate paper.  Do not abuse a calculator.

 

1.      Evaluate  around the ellipse , ,  

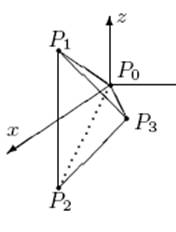
2.      Consider a tetrahedron with vertices at P₀ = (0, 0, 0), P₁ = (1, 0, 1) , P₂ = (1, 0,  1) ,
and  P₃ = (1, 1, 0).  Find the flux of  through

a.       the face P₀P₁P₂.

b.      the face P₀P₁P₃.

3.      Let  

a.       Calculate  and describe the gradient field geometrically.

b.      Calculate the flux of  over a sphere of radius a centered at the origin.

c.       Show that . 
Does the result of (b) then contradict the divergence theorem (Gauss’ Theorem) ?  Explain.

4.      Show that

5.      Evaluate the surface integral  where S is the helicoid with vector equation
 and .

6.      Let  

a.       Compute, in terms of the constants a and b the work done by the vector field  along the
portion of the helix  from (1,0,0) to (1,0,2π)

b.      Compute .  Show that  is conservative only if a = 1 and b = 2.

c.       Find the potential function for  using a = 1, b = 2 and verify your answer to part (a)
using the Fundamental Theorem of Calculus.

 

7.      Evaluate  where S is the part of the plane z = x  that lies above the square
with the vertices (0,0),  (1,0), (0,1) and (1,1).

8.      Let ,  Evaluate  where C is the elliptical path  

 

Math 2A  Chapter 13 Test  Fall 07.                      Name______________________________

Show your work for credit.  Write all responses on separate paper.  Do not abuse a calculator.

 

1.      Evaluate  around the ellipse , ,
SOLN:   

2.      Consider a tetrahedron with vertices at P0 = (0, 0, 0), P1 = (1, 0, 1), P2 = (1, 0,  1) , and P3 = (1, 1, 0).  Find the flux of  through a.       the face P0P1P2. SOLN:  This face is contained in the xz-plane and since the field vectors are parallel to this plane, there is no flux through that plane. b.      the face P0P1P3. SOLN:  A normal to this face is . Thus

As a follow-up, it may be noted that the flux through the face P₀P₂P₃ is also 1/6, by symmetry.  Thus, if
Gauss’ divergence theorem is to be believed, since the divergence of the vector field is zero, the flux
through the face P₁P₂P₃ must be 1/3.  Let’s see:  , so the unit normal is  which makes sense since this face is in the plane x = 1.   So the flux through that face is
indeed  

3.      Let  

a.       Calculate  and describe the gradient field geometrically.
SOLN:   

b.      Calculate the flux of  over a sphere of radius a centered at the origin.
SOLN:   

c.       Show that . 
Does the result of (b) then contradict the divergence theorem (Gauss’ Theorem) ?  Explain.
SOLN: 
The equation of the divergence theorem is that  which in this case evidently
leads to the contradiction, .  However, this does not contradict the theorem since a premise
of the theorem is that the vector field have continuous partial derivatives on an open region
containing E.  This vector field is not even defined at the origin, never mind having continuous
partials.

4.      Show that
SOLN:   

5.      Evaluate the surface integral  where S is the helicoid with vector equation  and .
SOLN:   

6.      Let  

a.       Compute, in terms of the constants a and b the work done by the vector field  along the
portion of the helix  from (1,0,0) to (1,0,2π)
SOLN:   

b.      Compute .  Show that  is conservative only if a = 1 and b = 2.
SOLN:   only if a = 1 and b = 2.

c.       Find the potential function for  using a = 1, b = 2 and verify your answer to
part (a) using the Fundamental Theorem of Calculus.
SOLN:   

 

7.      Evaluate  where S is the part of the plane z = x  that lies above the square
with the vertices (0,0),  (1,0), (0,1) and (1,1).
SOLN:   

8.      Let ,  Evaluate  where C is the elliptical path
SOLN:  This is (almost obviously) the gradient field for the potential function , thus
it is a conservative vector field and the path integral around any closed path is zero.  It’s also possible to
compute the curl, which is also the zero vector.

9.  
10. Another statement of Stokes’ theorem goes like this:
    Let S be the graph of the function z = f (x, y) , where f(x, y) is defined on some region S* for which
    Green’s Theorem is true. Further, let
    
     be a vector field
    on S. Then, under suitable differentiability and orientation assumptions, the following holds
    
    
     
    Where the directional cosine version of the unit normal,
    
     is used.
    Proof:  According to the hypotheses, the surface S is given by z = f (x, y) where  f (x, y) is defined on
    some region S* in which Green’s theorem is true.  Let
    
     be the vector field on  S* given by 
    
    
    
    
    Note that this means  
    
11. Since
    
     where
    
    , the work done by the force field
    
     in moving an object from
    
     to
    
     is
    
    .
    
    
    
12. If
    
     then the counterclockwise circulation of
    
     around the triangle with vertices
    
     is, by Green’s theorem,
    
    ..Joule, or some of energy.  The outward flux is
    
    .
    
    
    
13. a)  A field is conservative if its curl is zero.  Here,
    
    , so yes, it’s conservative.
    
    b)  For
    
    ,
    
    
    
    
    
14. The line segment  joining
    
     and
    
     can be parameterized by
    
    ,
    
    .  Thus
    
    .
    
    
    
    
    
    
    
15. The sphere can be parameterized by
    
     so that a normal vector is given by
    
    
    
    .  Evaluating the vector field
    
     on the surface of the sphere we have
    
    
    So the integrand for the flux integral is
    
    
    
    . 
    Thus the flux is
    
    
    
    
    
16. The divergence (Gauss’) theorem says that the flux is
    
    
    
    
    
    .
    
    
    
17. By Stoke’s theorem,
    
    
    
    
    
    .