|
Math 2A
1.
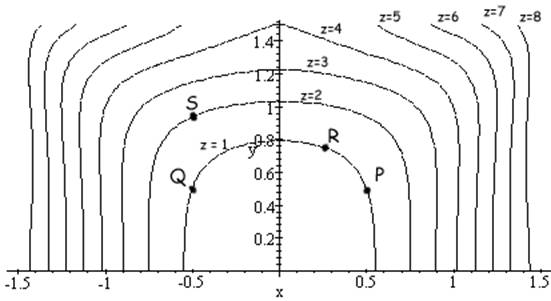
Level curves of a function 2.
Consider a.
Show that this function satisfies the equation: b.
Draw overlaid graphs lines for c. What effect does the parameter c have on the position of these graphs? d. 3.
Consider a.
Find 4.
Estimate 5.
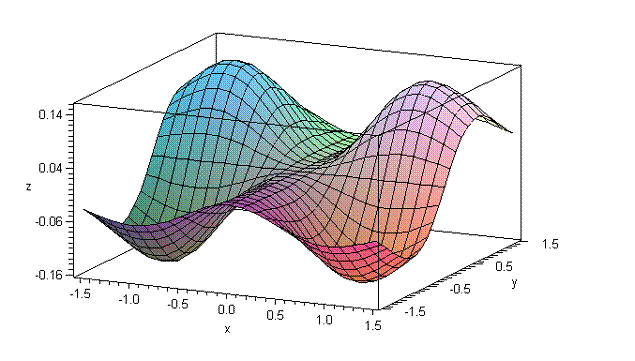
Consider the surface 6.
A rectangular beam, supported at its two ends, will
sag when subjected to a uniform load.
The amount of sag is modeled by the formula a. Determine dS for a beam 4 meters long, 0.1 meters wide, and 0.2 meters high, subjected to a load of 100 N/m. b. What conclusions can be drawn about the beam from the expression for dS? That is, which variables increase or decrease the sag? c.
For which variables is the sag most sensitive? For which variables is it the least
sensitive? 7.
The depth of a pond at (x, y) is given by h(x, y)
=12.69 a.
If a boat at (0.23, 1.44) is sailing in the direction
b. In what direction should the boat head to remain at a constant depth?
8.
Consider the surface a. Find the equation of the of the tangent plane at ( 3,1,-2) in two different ways: first, by viewing the surface as the level surface of a function of 3 variables, (x, y, z); second, by viewing the surface as the graph of a function of two variables z = f(x, y). b.
Find all points on the surface where a vector perpendicular
to the surface is parallel to the x-y plane. 9.
If f(x,
y) is a function of x and y and g(u,v)
= f( eu sin v,eu cos v),
find gu(0, 0)
given
10. Consider
the surface a.
Find an equation for the tangent plane at b.
What is the maximum rate of change of z per horizontal change as a point
moves along the surface from 11. Consider
the surface a. Find the vector which is normal to the surface at (1,0,1). b. For what values of y is the normal to the surface parallel to the xy-plane? c.
What is the instantaneous rate of change in z as a point moves along the surface
from (1,0,1) in the direction of (10,20,1) . 12. The
displacement of a string of length L
= 34 inches at time t and a
distance x from one endpoint is
given by a.
Consider a point initially at the center of the
string after 1/440 of a second. 13. Suppose
z = x3y2
and x = eu while y =
uew. Find zw(1,1). 14. Find
the local max and min and saddle points of the function 15. If
R is the total resistance of three
resistors, connected in parallel, with resistances R1, R2
and R3, then
|