Math 2A Vector Calculus
Final Exam
Fall ’07 Name_________________
Show all work on these pages. Do not abuse a calculator.
1.
Given points A(1,0,1),
B(2,3,0), C( 1,
1, 4) and D(0,3,2), find the volume
of the parallelepiped with adjacent edges AB,
AC, and AD. Hint: The volume of the
parallelepiped determined by vectors
is the triple product,
.
2.
Consider the lines and
.
a. Show that these lines intersect by finding the point of intersection.
b.
Find an equation for the plane containing these lines.
3.
Let . Give an approximate formula for the small
change
that results from small changes
and
in the values of x and y. Use this to approximate the value of 1.993.02.
|
4.
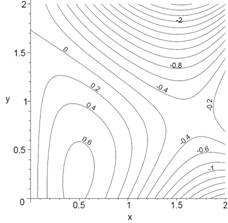
The figure at right is the contour plot of a function
of two variables, a.
Use the
contour plot to determine whether fx
and fy are > 0, = 0,
or < 0 b.
The function plotted on the figure is c. In the diagram, there are three places where the tangent plane is horizontal. Find the exact coordinates of each of these and characterize each as a max, a min or neither. |
|
5.
Consider the curve
a.
Find the length of the curve from
b. Find the curvature as a function of t.
c.
Find the tangential and normal components of the
acceleration.
6.
Consider
a.
Find a unit vector in the direction from (2, 1,
1) in which g decreases most rapidly.
b.
Find a parameterization of the line from that point in
the direction of most rapid decrease.
7.
Let and
. Use the method of Lagrange multipliers to
find the minimum and maximum values, if they exist, of
subject to the constraint
with
x > 0. In the case that they do exist, identify all
of the points (x, y) at which these values are attained.
8.
Find the area of the part of the saddle z =
x2 y2
that lies inside the cylinder x2 + y2 = 4.
9.
Let ,
and C be y2 = x,
between (1,
1)
and (1,1), directed upwards.
a.
Calculate .
b.
Calculate the integral three different ways:
i. directly;
ii. by using path-independence to replace C by a simpler path.
iii.
by using the Fundamental Theorem for line integrals.
10. Verify
Green’s theorem in the normal form, i.e. ,
by calculating both sides and showing they are equal if
and C
is the square with opposite vertices at (0,0) and (1,1).
|
11. Verify
Stokes’ theorem for the paraboloid
|
|
12. Use
the divergence theorem to calculate where V
is the region bounded by the cone
and the plane z = 1. To do this, you will
need a simple field whose divergence is `1.
How about
? Hint:
You can parameterize the cone by
.
Math 2A Vector Calculus
Final Exam Solutions
Fall ’07
1.
Given points A(1,0,1),
B(2,3,0), C( 1,
1, 4) and D(0,3,2), find the volume
of the parallelepiped with adjacent edges AB,
AC, and AD. Hint: The volume of the
parallelepiped determined by vectors
is the triple product,
.
SOLN: Take ,
and
so that
2.
Consider the lines and
.
a.
Show that these lines intersect by finding the point of
intersection.
SOLN:
b.
Find an equation for the plane containing these lines.
SOLN: Take one vector along r1;
and another along r2:
,
whence a normal to the plane is given by
,
so that the equation of the plane is
3.
Let . Give an approximate formula for the small
change
that results from small changes
and
in the values of x and y. Use this to approximate the value of 1.993.02.
SOLN: ,
so
and
. Thus, near a point
(x0, y0), with and
we have
. Thus
To be sure, this estimate is slightly above the TI86 approximation
|
4.
The figure at right is the contour plot of a function
of two variables, a.
Use the
contour plot to determine whether fx
and fy are > 0, = 0,
or < 0 at (1, 1.5) and (1.2, 0.6). b.
The function is |
|
SOLN: and
whence
,
,
c.
In the diagram, there are three places where the
tangent plane is horizontal. Find the
exact coordinates of each of these and characterize each as a max, a min or
neither.
SOLN: First find critical points where and
. For the latter,
. Now x
= 0 means that
and x =
2y also means that
. Thus there are three critical points:
and
. It is evident from the level curves plot that
is a local max and
is a saddle.
The point
on the y-axis
is not so obvious so we look at the discriminant:
,
and
so that at
,
this is also a saddle. I thought it’d be.
5.
Consider the curve
a.
Find the length of the curve from
SOLN:
b.
Find the curvature as a function of t.
SOLN:
c.
Find the tangential and normal components of the
acceleration.
SOLN: ,
6.
Consider
a.
Find a unit vector in the direction from (2, 1,
1) in which g decreases most
rapidly.
SOLN: .
b.
Find a parameterization of the line from that point in
the direction of most rapid decrease.
SOLN:
7.
Let and
. Use the method of Lagrange multipliers to
find the minimum and maximum values, if they exist, of
subject to the constraint
with
x > 0. In the case that they do exist, identify all
of the points (x, y) at which these values are attained.
SOLN: At the optimal point we require
that the normals are parallel:
Also, the constraint must be met. Thus
we have three equations in three unknowns:
From the last equation we substitute xy
= 1 into the second equation and get λx = 4 whence y = λ/4
and substituting into the first equation yields so that
and, correspondingly,
.
is a max and
is a min.
8.
Find the area of the part of the saddle z =
x2 y2
that lies inside the cylinder x2 + y2 = 4.
SOLN: so that
A =
9.
Let ,
and C be y2 = x,
between (1,
1)
and (1,1), directed upwards.
a.
Calculate .
SOLN:
b.
Calculate the integral three different ways:
i.
directly;
ii.
by using path-independence to replace C by a simpler path.
SOLN: The simpler path would be as t
goes from
1
to 1.
iii.
by using the Fundamental Theorem for line integrals.
SOLN:
10. Verify
Green’s theorem in the normal form, i.e. ,
by calculating both sides and showing they are equal if
and C
is the square with opposite vertices at (0,0) and (1,1). Parametrize the four edges like so:.
whence
and the normal components for these are
SOLN:
=
|
11. Verify
Stokes’ theorem for the paraboloid
|
|
12. Use
the divergence theorem to calculate where V
is the region bounded by the cone
and the plane z = 1. To do this, you will
need a simple field whose divergence is `1.
How about
? Hint: You can parameterize the cone by
.
SOLN: is the volume of the cone. To apply Guass’ theorem, compute
where S1
is the flat top of the cone and S2
is the curved surface of the cone. Now
since the normal to flat part of the surface is perpendicular to the field
lines, the first integral is zero. For
the second, we have the normal to the surface,
which points upwards when we want something
pointing outwards. So we negate it and
integrate
- Suppose
a triangle has coordinates (1,0),
and
.
Show that these lines are coplanar and find an equation for the plane that cont
- Use
Lagrange multipliers to seek the minimum value of
for which
.
c. Show
that the system of equations you arrive at implies that either or y
+ z = 0.
Assume that y + z
= 0 and show this leads to . You needn’t solve the equation.
- Suppose
a triangle has coordinates (1,0),
and
.
Show that these lines are coplanar and find an equation for the plane that cont
- Use
Lagrange multipliers to seek the minimum value of
for which
.
d. Show
that the system of equations you arrive at implies that either or y
+ z = 0.
Assume that y + z
= 0 and show this leads to . You needn’t solve the equation.