|
Math 2A - Chapter 12 Test Show your work for credit. Write all responses on separate paper. Do not use a calculator.
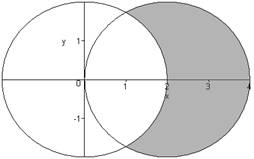
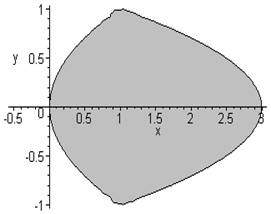
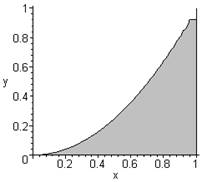
1. Write each area as an iterated integral. You do not need to compute its value. a.
b.
The area of the region inside the circle
2.
Interpret the integral 3.
Find the volume of the region E = 4.
Suppose a mass density function a. Find the mass of this laminar region. b.
Find the x-coordinate
of its center of mass. 5.
Evaluate 6.
Find the area of the surface z = x + y2 that lies above the triangle
with 7.
Evaluate 8.
Use cylindrical coordinates to evaluate 9.
Use spherical coordinates to evaluate 10. Use
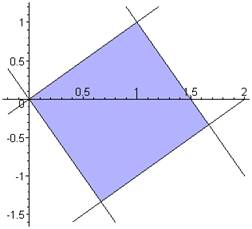
the given transformation to evaluate
|
|
Math 2A - Chapter 12 Test
Solutions
1. Write each area as an iterated integral. You do not need to compute its value. a.
2.
Interpret the integral 3.
Find the volume of the region E = 4.
Suppose a mass density function a.
Find the mass of this laminar region.
ANS: 7.
Evaluate 8.
Use cylindrical coordinates to evaluate 9.
Use spherical coordinates to evaluate
Corners of a rectangular region
in the uv-plane. Thus the integral is |