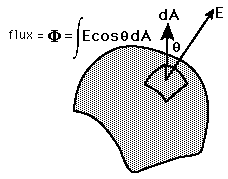Vector Calculus Links

http://butlercc.edu/mathematics/Utilities/tools_multivariable_knisley/ 

Nestled in the charming village of South Orange, New Jersey, Seton Hall University is only 14 miles from New York City, one of the world's most exciting cities and has a fine Math and Computer Science program.Their plotter is very nice, except that while you drag the surface plot, it disappears.

http://sciris.shu.edu/thinklets/Math/Calculus/SurfacePlotter/Surface.html 

MIT's math department has a collection of calculus pages here you can get into from here:
http://math.mit.edu/cgi-bin/classes.cgi .  Click on 18.02 for a collection of links to various vector calculus related documents.  You can also access the pull down box at the top to choose another term and a differential equations link such as http://www-math.mit.edu/18.013A/HTML/index.html
 

David Little at Penn State has a nice space curve applet you can also download locally, they say.  It shows little plane panels of the three x, y and z functions in windows at the top.
http://www.math.psu.edu/dlittle/java/calculus/spacecurves.html 

 

At Jackson State University, you can drag and see simultaneously!  http://cs.jsu.edu/mcis/faculty/leathrum/Mathlets/parapath.html 

Matthias Kowski at Arizona State University set up this interesting applet: a Vector Field Analyzer which can really help build your intuitive sense of vector fields and their equations.  Here are some links:  http://math.la.asu.edu/~kawski/vfa2/index.html

http://math.la.asu.edu/~kawski/

http://math.la.asu.edu/~kawski/conferences/99plymouth/proceedings/sld001.htm