Summer Enrichment

Circular Motion Lab

“An object that moves in a circle at constant speed v is said to

undergo uniform circular motion. Examples are a ball on the end

of a string revolved around one’s head.” –Douglas Giancoli

Purpose

This lab will allow us to examine the relationship between mass,
velocity, radius, and centripetal force.

Theory

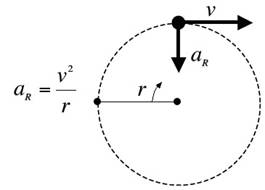
Newton’s Laws of Motion

1.    (The Law of Inertia)
Every object in a state of uniform motion tends to remain in that state of motion unless an external force is applied to it.

2.    (acceleration = F_net/mass)  The acceleration of an object produced by the sum of all forces acting on the object (the net force) is directly proportional to the magnitude of the net force, in the same direction as the net force, and inversely proportional to the mass of the object.

3.    For every action, there is an equal and opposite reaction.

When a mass on a string swings steadily around in a circle we call it uniform circular motion.  They speed is constant, but since the direction is continually changing, the velocity vector (the direction is changing) and a constant acceleration.  Even though the speed is constant, the velocity (speed and direction) is constantly changing and so the acceleration is not zero.  Since the velocity of the mass is always changing direction

toward the center of the circle. It follows then that the mass is always

accelerating toward the center of the circle. That “center-seeking”, radial, or

centripetal acceleration (a_R) is given by the following expression:

Your teacher will now prove this for you, so listen carefully, take good notes and ask questions about what you would like explained more better.

Newton’s second law is encapsulated in the formula

acceleration = (net force)/mass

or

The arrows are used to indicate that the force and the acceleration are vectors.  It is assumed that the mass is constant (this is crucial for the formula to work.)

So if you know the centripetal acceleration  you also know the centripetal force .

Materials (or improvise similar)

·         A piece of string, 1 to 1.5 meters long

·         Several washers or nuts to use as weights

·         Masking tape

·         Meter stick

·         Timer

Procedure

·         This lab requires you to swing masses on the end of a string with uniform circular motion to examine what happens as you change three quantities: the mass, the length of the string, and the velocity. That is, what happens to the centripetal force when you change v, r, and m? It makes sense to divide this lab into three parts that will examine each of these.

·         To get started, tie a knot at the end of your string that will act as a stop. It is important to make a good stop so that your masses do not fly off when you start swinging your string. We don’t want anyone getting hurt.

·         To calculate velocity, use your timer and the equation for the circumference of a circle (2πr). Note that to measure velocity you can approximate the time of one revolution as the average time of 10-20 revolutions.

·         A table is provided to help you organize your data. In the column labeled “Feel” of the Force, you will enter words like “greater, less, same.” You will put a word there that describes how the force of the rope in your hand feels compared to the initial force. Do an initial trial first to have a baseline, and then for each trial record whether the force is less, greater, or the same.

·         You may work through the three parts of this lab in any order you wish.

Part 1: How Mass Affects FC

In this experiment you will see how mass affects the centripetal force, Fc. You must hold the radius and velocity as constant as possible for this part so that you are only seeing what effect a change in mass produces. This will be hard to do and it may take a couple of trials to get it right. Experiment with different amounts of mass and try to feel how the force varies on your hand. Does the rope pull more or less on your hand when the mass at the end of the rope is increased?

Part 2: How Velocity Affects FC

In this experiment you must hold mass and radius constant. Spin the weight around in a circle and vary the velocity at which you spin it. Record how the amount of force on your varies with velocity.

Part 3: How Radius Affects FC

In this experiment you must hold mass and velocity as constant as possible. This will be hard to do and it may take a couple trials to get it right. First, measure a couple of lengths out from your knot and wrap some tape around the rope to mark the spots. Don’t go over 1.5 m, for the sake of safety. Spin the mass at different radii by changing the location of where you grab the rope. Once again, it is crucial that velocity is constant – pay attention to this.

Part 1
(Δmass)

Mass
(g)

Velocity
(m/s)

Radius
(m)

“Feel” of the force

Calculated
Fc (N)

Initial

X

Trial #1

Trial #2

Trial #3

Part 2
(Δvelocity)

Mass
(g)

Velocity
(m/s)

Radius
(m)

“Feel” of the force

Calculated
Fc (N)

Initial

X

Trial #1

Trial #2

Trial #3

Part 3
(Δradius)

Mass
(g)

Velocity
(m/s)

Radius
(m)

“Feel” of the force

Calculated
Fc (N)

Initial

X

Trial #1

Trial #2

Trial #3