Physics 5 Assignment for Week 12

Basins of Attraction and Roots of Unity in the Complex Plane.

 

The n roots of  unity (1) are the n solutions to the equation   These roots are distributed evenly around the unit circle in the complex plane so that the kth root is the complex number,   where .  

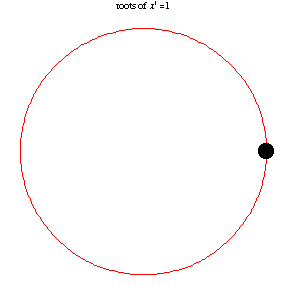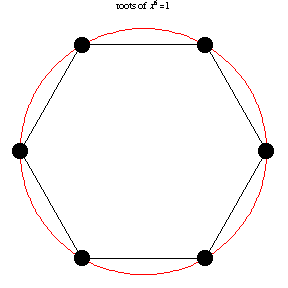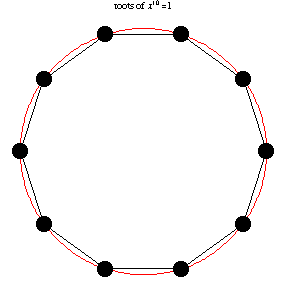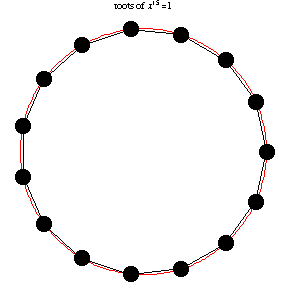
These problems investigate the dynamics of searching for complex roots of unity in the complex plane.

1.      Write a C++ program which uses the Complex class you built for chapter 6 exercise 6 to iterate the Babylonian algorithm:
                           
for complex iterates, x_k.  The program should prompt the user for a natural number n > 2 (and reject values that don’t fit this criterion) and then prompt the user for real and imaginary parts of the initial complex number x₀ in the series.  The program then should report back the complex root of unity that the Babylonian algorithm converged to, its polar angle and the number of iterations required. 
Submit this program as <yourname>-wk12-1.cpp

2.      Write a C++ program that creates a two dimensional array of 600X800 evenly distributed points in the rectangle  and  and assigns to each point in the array the index  of the polar angle of the 5^th root of unity to which the Babylonian algorithm converges with n = 5, using the corresponding coordinates of the initial point as the initial value for iteration. Read about how to open a file stream (chapter 14) and open a file called, say, data.dat, and write these 600*800 values to the file.  Submit this program as <yourname>-wk12-2.cpp