Physics 5
|
|
void setReal(float r) {_real = r;} void setImag(float i) {_imag = i;} float getReal() {return _real;} float getImag() {return _imag;} |
Then this fairly simple DarkGDK() function:
|
void DarkGDK() {
float R,I,a,b; Complex x(1,1),xNext,c; int count; //dbWaitKey(); // The game loop while ( x.sqrModulus()>.0001 ) { dbSetCursor(0,0); dbInk(white,black); dbPrint("Enter the real and imaginary parts of a complex number z with |z| < 5.2."); R = atof(dbInput()); I = atof(dbInput()); x.setReal(R); x.setImag(I); c = x; xNext = x*x + c; count = 0; while((x-xNext).sqrModulus()>0.0001 && count < 50) { x = xNext; dbInk(dbRGB(10*count,10*count,10*count),black); a = (int)(629*(x.getReal()+2)/4); b = (int)(479*(x.getImag()+2)/4); dbBox(a,b,a+5,b+5); dbWaitKey(); xNext = x*x + c; // Mandelbrot iteration ++count; } dbClear(0,0,0); } } |
A key part of this
loop is the scaling formula used to convert from the Complex number to a
point on the dbScreen:
a = (int)(629*(x.getReal()+2)/4);
b = (int)(479*(x.getImag()+2)/4);
Which makes the dbBox color lighter and lighter as they
progress. Here is one output of the
program (it has been inverted so the boxes get darker) with the initial point
-0.7 + 0.3i point just barely outside the Mandelbrot set,
so the iteration diverge outward:

This prompted a few changes in the code making the dbBox a bit smaller and tweaking
the colors a bit:
|
while((x-xNext).sqrModulus()>0.0001 && count < 100) { x = xNext; dbInk(dbRGB(10+2*count,250-2*count,50+2*count),black); a = (int)(629*(x.getReal()+2)/4); b = (int)(479*(x.getImag()+2)/4); dbBox(a,b,a+2,b+2); dbWaitKey(); xNext = x*x + c; // Mandelbrot iteration ++count; } |
Which lead to this output:
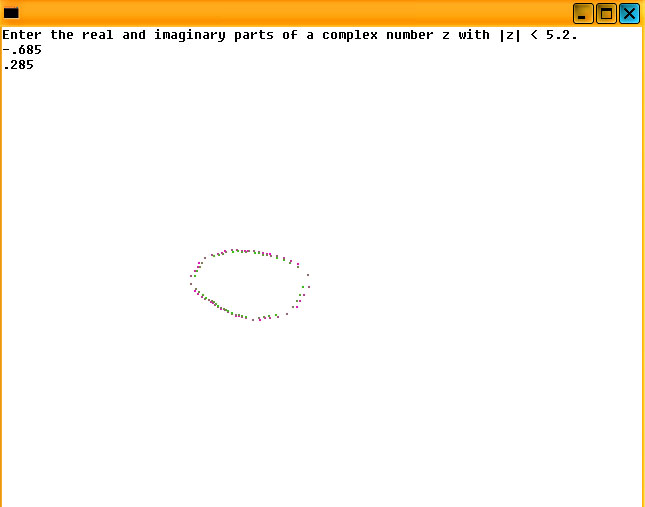
This led to another variation,
|
dbInk(white,white); x = xNext; //dbInk(dbRGB(10+2*count,250-2*count,50+2*count),black); a = (int)(629*(x.getReal()+1)/2); b = (int)(479*(x.getImag()+1)/2); dbBox(a,b,a+1,b+1); xNext = x*x + c; // Mandelbrot iteration ++count; if(count%10000==0) dbWaitKey(); } |
Again the picture is inverted to black on white instead of white on black.
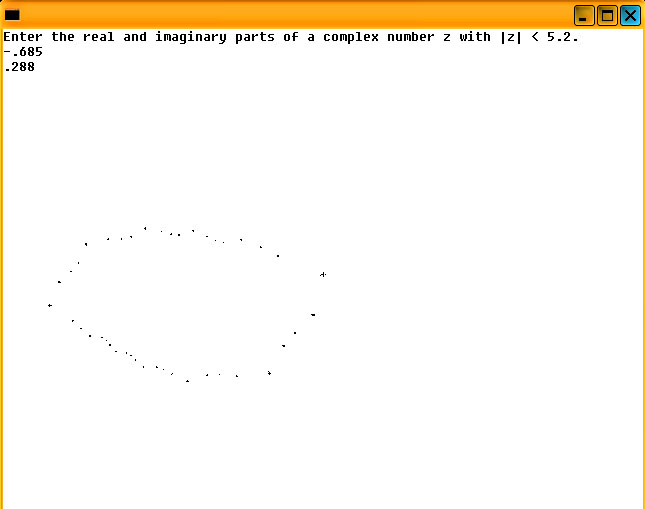
Another rendition of the loop:
|
while((x-xNext).sqrModulus()!=0.0 && x.sqrModulus() < 10 && count < 10000) { x = xNext; a = (int)(629*(x.getReal()+1)/2); b = (int)(479*(x.getImag()+1)/2); dbBox(a,b,a+1,b+1); xNext = x*x + c; // Mandelbrot iteration ++count; if(count%200==0) { // Every 200th iteration x.print(10,10); // It’s helpful to see the values xNext.print(10,20); // and pause. dbWaitKey(); dbInk(black,black); // Paint over the old values. dbBox(0,13,360,60); dbInk(white,black); } // end if } // end while |
With the initial value -0.688+0.28i, the first 10000 iterates are plotted below.
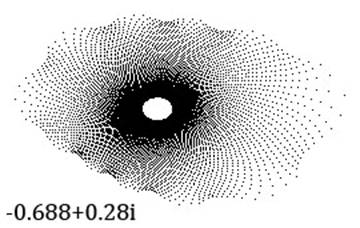
This point is near the boundary of the Mandelbrot set and on the interior, so it takes many iterations to converge to a point somewhere near the center of the white spot in the middle. Going a tad further downwards towards the border produces a divergent orbit:
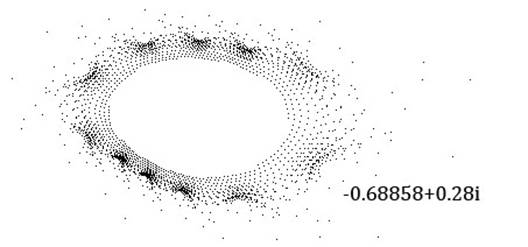
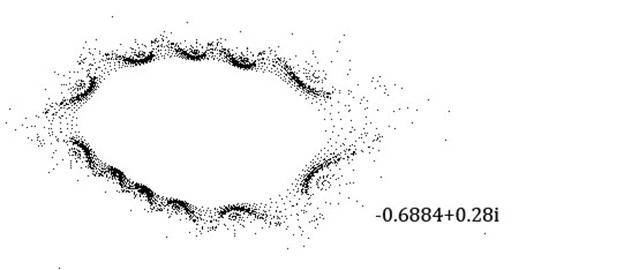


That appears to be right near the boundary…is it repeating points exactly, or only approximately?

Mandelbrot with his hair on fire.
So what’s going on here? For
those, like me, who are interested here’s a bit of theory.
As H.-O.Peitgen and H.R.Richter wrote in their monograph of 1986, The Beauty of Fractals, The Mandelbrot set embodies a transition from order to chaos. [..] Think of attractors as points in the plane competing for influence on other points in the plane: if an initial point x0 leads to convergence of the Mandelbrot iterates xn+1 = x2n + c to a point inside the plane, then x0 is said to be in the basin of attraction for the point c. This basin must also include all the inverse iterates (preimages) of x0. The boundary such a basin of attraction is an intricate curve or sequence of curves that may or may not be connected. The orbit of a point on the boundary of a a Julia set will include other points on the boundary, none of which are in one basin of attraction or another and so flitter about with seemingly random abandon. Further, Peitgen and Richter put it,
It can happen
that the boundary falls to dust, and this decay is one of the most
important scenarios.
Mandelbrot’s iteration formula is very simple:
Consider the very simple case where c = 0. Then there are three cases:
· If |x0| < 1 then xn → 0 as n →∞
· If |x0| > 1 then xn → ∞ as n →∞
· If |x0| = 1 then |xn| = 1 as n →∞ and the sequence stays on…but may hop about on the boundary.
Consider, for instance, the value c
= -0.12375 + 0.56508i and the iterates for each x0 in the complex
plane. If the iterates for a
particular x0
diverge to infinity then x0 is not in the
basin of attraction for this c,
whereas if the iterates don’t diverge (which can mean either (1) converging
to a fixed point or (2) cycling through a finite set of points or wandering
aimlessly within a fixed region) then the boundary of the basin of attraction
is on or more closed curves with an intricate shape: a fractal. Boundaries of this kind are known as Julia
sets after the French mathematician Gaston Julia. The Julia set contains the unstable fixed
point of the mapping
together with all of its preimages; it contains
an infinite number of unstable periodic sequences also with their preimages,
and above all it contains chaotic sequence of points that never approach any
kind of regularity.
As an example, try x0 = c = -0.12+0.74i. This leads to the first iterate c2 + c = 0.0995+0.005265i and (c2 + c)2 + c = -0.653+0.563i and ((c2 + c)2 + c)2+c = -0.1199+0.7399i brings us back (nearly exactly) to where we started: this is a three-cycle. The basin of attraction of this three-cycle is not a single closed curve (as in the previous case) but infinitely many intricate closed curves. Here’s the Julia fractal followed by the code I used to produce it:
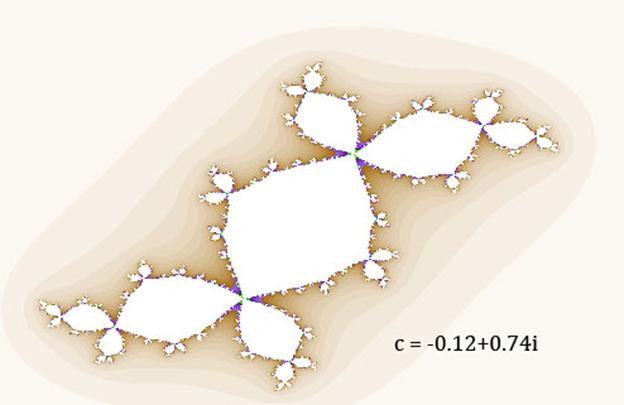
|
void DarkGDK() { float R,I,a,b; Complex x(1,1),xNext,c; int count; while ( 1 ) { dbSetCursor(0,0); dbInk(white,black); dbPrint("Enter real & imag for z near M's bndry:"); R = atof(dbInput()); I = atof(dbInput()); c.setReal(R); c.setImag(I); if(c.sqrModulus()==200) break; // exit condition dbInk(white,black); for(int i = 0; i < 640; ++i) { for(int j = 0; j < 480; ++j) { x.setReal((float)i/160-2.); x.setImag((float)j/120-2.); count = mandelbrot(x,c); if(count==0) { dbInk(white,white); dbBox(i,j,i+1,j+1); } else { dbInk(dbRGB(255-5*count,255-8*count,255-13*count),white); dbBox(i,j,i+1,j+1); } } // end for } //end for dbWaitKey(); dbClear(0,0,0); } //end while } //end DarkGDK()
int mandelbrot(Complex x, Complex c) { Complex seed = c; Complex xTemp = x*x + seed; int count = 0; while(count < 100) { ++count; x = xTemp; xTemp = x*x + seed; if(xTemp.sqrModulus() > 10) return count; } return 0;// } |