Math 5 Trigonometry  Final Exam Problems  Fall ’07

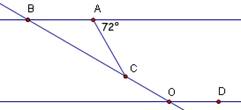
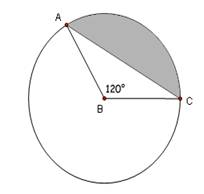
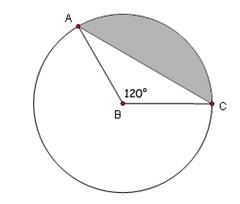
1.      In the diagram at right, assume that  and that AB = AC. a.       What is the degree measure of ? b.      If OB = 100, then how far apart are the parallel lines?  2.      Central angle  is swept out in the unit circle as shown at right. a.       If B is at the origin and C is at (1,0) in a rectangular coordinate system, what could the coordinates of A be? b.      What is the length of AC?  c.       What is the area of the shaded region?

3.      Given   a.       Find a formula for the inverse function. b.      Graph  and  together, showing symmetry across the line y = x.

 

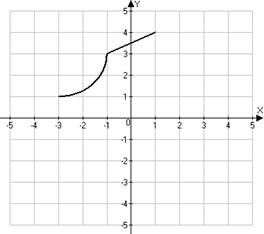
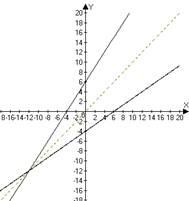
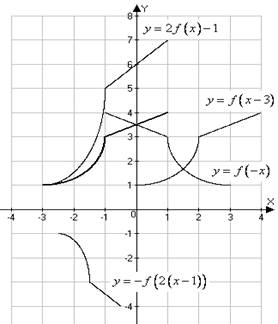
4.      Given the graph of  shown at right, draw graphs of each of the following functions: a.         b.        c.         d.

5.      If  and the terminal point determined by t is in the 2^nd quadrant, find each of these:

a.       .           

b.      . 

c.          

d.        

6.      Sketch a graph for the sinusoidal function . 
Also, state the period, amplitude and phase angle. 

7.      Find the side labeled x:

a. 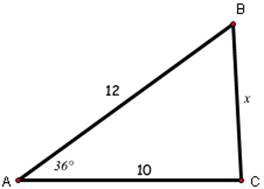            b.   

 

8.      Consider the vectors  and  

a.       Draw the vectors together in the coordinate plane (take the origin as the original point for each).

b.      Use the formula  to approximate (four digits) the radian measure of the angle
between these vectors.   

c.       Find the length of

9.      Consider  

a.       Find the domain of the function. 

b.      Find the range of the function.

c.       Sketch a graph of the function showing two periods.

10.  A potter’s wheel with radius 6 inches spins at 180 rpm.  Find the angular and linear speeds of a point
 on the rim of the wheel in feet per second.

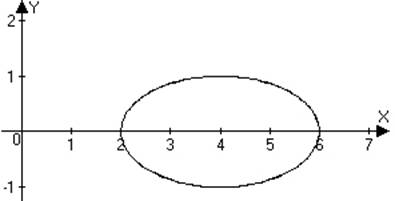
11.  Write the conic in standard form and sketch a graph indicating key features:

a.      

b.     

 

 

Math 5 Trigonometry  Final Exam Solutions  Fall ’07

12.  In the diagram at right, assume that  and that AB = AC. a.       What is the degree measure of ? SOLN:   and  is isosceles so  This means that the alternate interior angle at O is also 36° so that  = 144° b.      If OB = 100, then how far apart are the parallel lines?  SOLN:  13.  Central angle  is swept out in the unit circle as shown at right. a.       If B is at the origin and C is at (1,0) in a rectangular coordinate system, what could the coordinates of A be? SOLN:

b.      What is the length of AC?  SOLN:  

c.       What is the area of the shaded region?  SOLN:  Area of sector  area of triangle =  

14.  Given   a.       Find a formula for the inverse function. SOLN:    b.      Graph  and  together, showing symmetry across the line y = x. SOLN:  Shown at right.

 

15.  Given the graph of  shown at right, draw graphs of each of the following functions: a.         b.        c.         d.

16.  If  and the terminal point determined by t is in the 2^nd quadrant, find each of these:

a.       .            SOLN:   

b.      .            SOLN:   

c.          SOLN:   

d.        SOLN: 

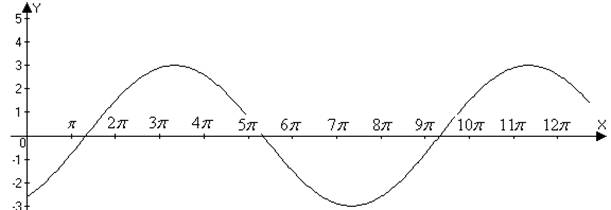
17.  Sketch a graph for the sinusoidal function .  Also, state the period, amplitude
and phase angle.  SOLN:  Period = 8π, amplitude = 3 and phase angle = 4π/3.

18.  Find the side labeled x:

a.             b.    
(a) 
(b)   

 

19.  Consider the vectors  and  

a.       Draw the vectors together in the coordinate plane (take the origin as the original point for each).
SOLN: 

b.      Use the formula  to approximate (four digits) the radian measure of the angle
between these vectors.    
SOLN:   

c.       Find the length of
SOLN: 

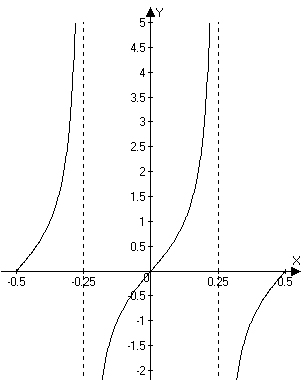
20.  Consider  

a.       Find the domain of the function.  Coup de tat
SOLN:  The domain of the function is  where  

b.      Find the range of the function.
The range is all reals,  

c.       Sketch a graph of the function showing two periods.

21.  A potter’s wheel with radius 6 inches spins at 180 rpm.  Find the angular and linear speeds of a point
on the rim of the wheel in feet per second.
SOLN: 

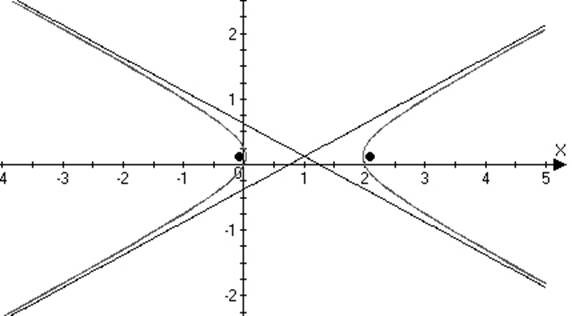
22.  Write the conic in standard form and sketch a graph indicating key features:

a.      
SOLN: 
whence the center is , , , , vertices are at  and the asymptotes are along

b.     
SOLN:   This is equivalent to , which means that a = 2, b = 1 and so .

Major axis vertices are at (0,2) and (0,6) while minor axis vertices are at (4,1) and (4, 1).