Math 5  Trigonometry  Chapter 6 Test  Fall ’07  Name________________________

Show your work for credit.  Write all responses on separate paper.  Do not abuse a calculator.

 

 

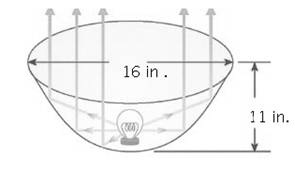
1.      A light bulb is to be placed at the focus of a parabolic dish as shown in the figure at right.  How high above the bottom should the light be placed? 2.      Find an equation for the ellipse with foci  and vertices .

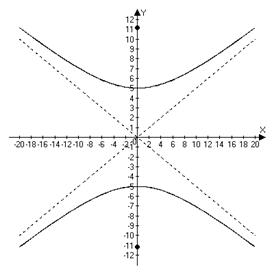
3.      Find the vertices, foci, and asymptotes of the hyperbola  and sketch a
graph illustrating these features.

4.      Find an equation for the hyperbola with asymptotes  and vertices at

a.        

b.       

5.      Complete the square to determine whether the equation represents an ellipse, a parabola, or a
 hyperbola.  If the graph is an ellipse, find the center, foci, eccentricity and endpoints of the
major and minor axes.  If it is a parabola, find the vertex, focus and directrix.  If it is a
hyperbola, find the center, foci, vertices and asymptotes.

a.        

b.       

c.      

6.      If the coordinate axes are rotated through an angle of 60°.  Find the new coordinates of the
point (3,5).

7.      Use the discriminant to determine whether 2y² + 5xy + 2x² = 4x describes a parabola, ellipse or
hyperbola.

8.      Find the angle of rotation of axes to eliminate the xy  term in the following equations.  Write
the angle in radians and approximate with 4 significant digits.

a.        

b.       

9.      Find parametric equations to describe the hyperbola  

 

10.  Write the equation for the conic section described by  in rectangular form.

 

 

Math 5  Trigonometry  Chapter 6 Test Solutions.

 

 

1.      A light bulb is to be placed at the focus of a parabolic dish as shown in the figure at right.  How high above the bottom should the light be placed? SOLN:  If the parabola is opening upwards from a vertex at (0,0), then it has the form 4py = x2, whence 44p = 64 and the distance from the focus to the vertex is p = 16/11.

2.      Find an equation for the ellipse with foci  and vertices .
SOLN:  b² = a²  c² = 11²  10² = 21 so the equation is  

3.      Find the vertices, foci, and asymptotes of the hyperbola  and sketch a graph illustrating these features. SOLN:   has vertices at  foci at   The asymptotes are   4.      Find an equation for the hyperbola with asymptotes  and vertices at a.         So we know the ratio of b/a = 2/3 and that b = 3.  Thus a = 9/2 and the equation is

 

b.       Here a = 3 so b = 2 and the equation is simply  

5.      Complete the square to determine whether the equation represents an ellipse, a parabola, or a
hyperbola.  If the graph is an ellipse, find the center, foci, eccentricity and endpoints of the
major and minor axes.  If it is a parabola, find the vertex, focus and directrix.  If it is a
hyperbola, find the center, foci, vertices and asymptotes.

a.        is an ellipse with center (3,0), endpoints of minor axes at (0,0) and (6,0) and major axes at (3, 4) and (3, 4) with foci at   and eccentricity  

b.       is an ellipse with center
(-4,0), vetices (-4,1) and (-4,1), foci at   and asymptotes .

c.        is a parabola with vertex (4, 8), focus at
(4,0), directrix along y = 16.

6.      If the coordinate axes are rotated through an angle of 60°.  Find the new coordinates of the
point (3,5).
SOLN: 

7.      Use the discriminant to determine whether 2y² + 5xy + 2x² = 4x describes a parabola, ellipse or
hyperbola.
SOLN:  B²  4AC  = 25  16 > 0 so it’s a hyperbola.

8.      Find the angle of rotation of axes to eliminate the xy  term in the following equations.  Write
 the angle in radians and approximate with 4 significant digits.

a.      
SOLN:   

b.       
SOLN:   

9.      Find parametric equations to describe the hyperbola
SOLN:   

 

10.  Write the equation for the conic section described by  in rectangular form.