Math 5 – Trigonometry – Geometry Test Review Problems. 

 

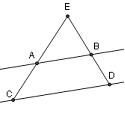
1.      Prove that if  is parallel to  then .

 

2.      Prove that the base angles of an isosceles trapezoid are congruent.  Use the result of #1.

 

 

3.      In any ΔABC, take E and D as points on the interior of segments AC and BC, respectively (see the figure.)  AF bisects , and BF bisects . 

a.       Prove that

b.      Prove this is true even if E coincides with C.

c.       Prove that this is true even if E and D are exterior points on the extensions of  AC and BC. 

 

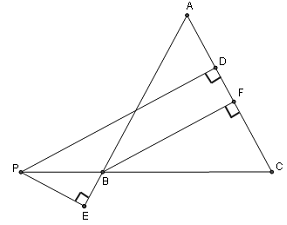
4.      In isosceles ΔABC (AB = AC), CB is extended through B to P (see figure.)  A line from P, parallel to altitude BF, meets AC at D, (where D is between A and F.)  From P a perpendicular line is drawn to meet the extension of AB at E so that B is between E and A.  Express BF in terms PD and PE.

 

Solution strategy: Start by looking for similar triangles.   In this case, an important similarity is established by noting that, since ΔABC is

isosceles,  and vertical angles  so right triangles ΔBFC and ΔPEB  have one of their acute angles congruent and so must be equiangular (since the sum of interior angles of any triangle is 180˚.)  Thus  and among the many proportionality equations we could write, consider  

(1.1)                         .

Now, if a line parallel to one side of a triangle and intersects the other two sides, as BF is parallel to PD  and intersects PC and DC, then the triangles are equiangular and so similar.  Thus , and again, .  This also means that

(1.2)                

Combining 1.1 and 1.2,

(1.3)                                          

Which means the numerators must be equal and so .  QED

 

Here’s an alternate proof, in the form of a sequence of problems:

 

Justify each of the following statements (refer to the statement of the problem preceding the first proof above.)

a.       PD is parallel to BF.

b.     

c.      

d.     

e.       Draw a line from B perpendicular to PD at G.  Then .

f.       

g.       BF=GD

h.