Play Algebra Arcade!
Here are some screen shots of Algebra Arcade, to give you some kind of idea of what it's about.This is the opening screen, showing the options for play: one or two players can play at a time.

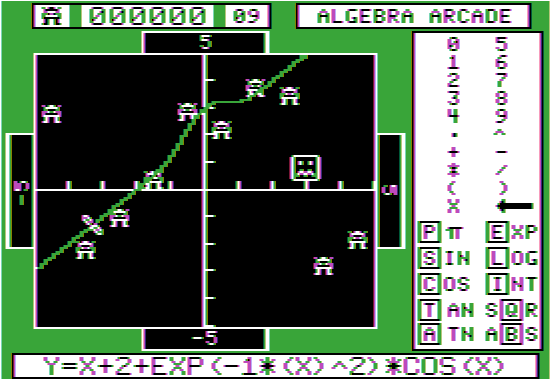 Here
is a rather bad attempt at defining a function to get the algebroids.
As you can see from the function y = x + 2 + exp(-x2)cos(x)
Here
is a rather bad attempt at defining a function to get the algebroids.
As you can see from the function y = x + 2 + exp(-x2)cos(x)
defined at the bottom of the screen, the concept was to draw a line (y
= x+2) passing through the three algebroids in the lower left and
then add a wobble to make the curve pass through more algebroids in the
center middle.
(The "-1*(X)^2" may seem peculiar: it's to get
around an error in the parser that interprets
"-X^2" as positive.) Well, as you can see,
the whirlwind (shown frozen here between the first two algebroids in the
lower left) missed the first two algebroids on the lower left (even though
it shaved the second one's antennae) and only wobbled through two of the
four algebroids in the center top. The function would be better with a
slightly greater slope and a higher frequency wiggle centered more on 1:
Y=1.2*X+2+2*EXP(-0.5*(X-1)^2)*COS(8*X)
As it is, the curve hit three algebroids, scoring 1200 = 200 + 400 + 600
(each additional hit is worth 200 more than the previous hit.)
If you want to set up Algebra Arcade on your PC, follow these steps:
- Download the Apple II Emulator here.
- Unzip the emulator to a directory of your choice and launch the setup file.
- Download the ALGEBRA.DSK file here.
- Unzip this file to whatever location is convenient.
- Simply double-click on the ALGEBRA.DSK file and the Apple II Emulator should launch algebra arcade.
Included with the the DSK file is the following document giving a description for Algebra Arcade which appeared in some magazine about 20 years ago:
About Algebra Arcade
What distinguishes this program is the way in which the topic is presented. After being shown a set of coordinates, a group of creatures called "algebroids" scurry onto the screen, scattering to various locations on the grid.
It is the user's task to come up with an equation which, when plotted, will pass through as many algebroids as possible. After the graph is plotted, a "whirlwind" follows the path of the graph, "knocking off" any algebroids through which it passes. Points are earned for each algebroid hit: 200 for the first, 400 for the second, and so on. However, the graph plotted must not hit the "shifty-eyed ghost" who also appears on the grid; if it does, the ghost turns into the dreaded Graph Gobbler who munches the equation, leaving the player scoreless.
The game can be played alone, or one-on-one. If, when playing against an opponent, the Graph Gobbler appears, the offending player is sent to "The Committee" which decides, randomly, if the player should be penalized one turn, three turns, or it's possible to get off without losing a turn.
Each player (in both the one- or two-player games) starts off with ten turns; an extra turn is added by scoring 10,000 points, clearing all the algebroids, or by finding the invisible Graph Gobbler. (Oh yes, we forgot to mention that when the tenth algebroid is eliminated, the Graph Gobbler "has a fit and disappears.")
At that time, the player has up to three tries to find the invisible Graph Gobbler by graphing equations. If one graph finds the hiding place, the player scores an additional 1000 points and earns an extra turn. But, if the player misses after all three attempts, he is sent to The Committee. When both players have used up all their turns, the one with the highest score is named the Algebra Arcade champion.
The program has several features which make it more enjoyable and challenging. It can be played either under keyboard control or by using a joystick; this is the first questions asked after the program is loaded. The program includes a Features Menu which can be used to change the characteristics of the game. Specifically, this menu includes the following options
-
Saving the current game on disk to continue it a later time.
-
Changing the coordinates of the grid: They are preset at -5 to the left and bottom and +5 to the right and top. They can be reset to any values, seven characters or less in length, which may include a decimal point or [pi].
-
Selecting certain equation families. The families include: the linear equation Y = MX + B, three different representations of a quadratic equation, a third degree equation, and an equation containing a sine function. An additional option allows you to build your own equation, using allowable symbols and functions which appear in a table on the display screen.
-
Playing the game with or without the Graph Gobbler.
-
Testing the length of a graph, to help determine the use of long, oscillating graphs which could make the game quite easy (although finding such graphs is no easy feat). This length test can be turned on or off.
-
Adding an internal timer to encourage quick thinking: if this option is chosen, the regular score is multiplied by a factor, dependent upon how quickly the equation was entered. The timer can be set to several speeds, or not used. If it is used, the algebroids change positions on the screen between turns. In an untimed game, algebroids not eliminated return to the same position at which they appeared during the previous turn.
If desired, these features can be changed as the game progresses. The options of coordinates and types of equations allow for a wide range of difficulty. High school freshmen can use this program to learn to plot straight lines, while seniors and even college students could use it to study the characteristics of higher degree, more complex equations. Thus, the package can be used by a student over a period of years, as his knowledge of mathematical concepts increases.
An additional option of the program is the use of a Practice Field on which equations can be tested before they are actually plotted on the playing field. In this way, a player who is just learning these skills can specify several different equations to be plotted on the practice field. By choosing values wisely, the player can gain valuable knowledge as to how various equations appear on the grid, so that when he or she chooses an equation to be plotted on the playing field, the number of points scored can be maximized.